Concise magnetic model for thermodynamic calculations of iron from 0 to 1800 K

Abstract

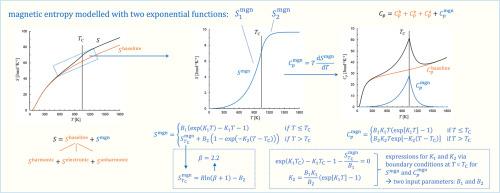
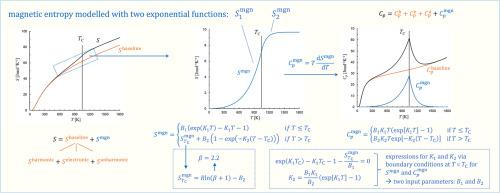
The proposed magnetic model represents magnetic entropy using two exponential functions: one for long-range order below the transition temperature and another for short-range order above it. This approach ensures that both the magnetic entropy and its temperature derivative approach zero smoothly as temperature nears absolute zero. Differentiating this expression yields a magnetic heat capacity curve with a lambda peak, defined by two adjustable parameters that control its temperature dependence on either side of the transition. This magnetic contribution is integrated with established components of heat capacity, including electronic, harmonic, and anharmonic lattice terms. The overall thermodynamic model was optimized using experimental data for bcc and fcc iron, encompassing transition temperatures, heat capacity measurements from 10 to 1800 K, enthalpy differences, Bohr magneton values, and the magnetic enthalpy fraction attributed to short-range order.