Boundary layer profiles of positive solutions for logistic equations with sublinear nonlinearity on the boundary

Abstract

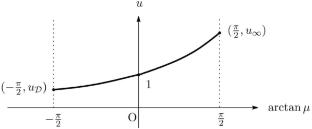
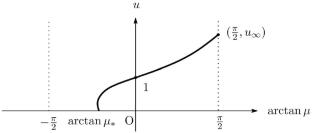
In this paper, we consider the logistic elliptic equation \(-\Delta u = u- u^{p}\) in a smooth bounded domain \(\Omega \subset {\mathbb {R}}^{N},\) \(N\ge 2,\) equipped with the sublinear Neumann boundary condition \(\frac{\partial u}{\partial \nu } = \mu u^{q}\) on \(\partial \Omega ,\) where \(0<q<1<p,\) and \(\mu \ge 0\) is a parameter. With sub- and supersolutions and a comparison principle for the equation, we analyze the asymptotic profile of the unique positive solution for the equation as \(\mu \rightarrow \infty .\)