Categorical pentagon relations and Koszul duality
Abstract
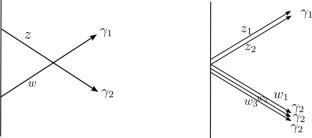
The Kontsevich–Soibelman wall-crossing formula is known to control the jumping behaviour of BPS state-counting indices in four-dimensional theories with \(\mathcal {N}=2\) supersymmetry. The formula can take two equivalent forms: a “fermionic” form with nice positivity properties and a “bosonic” form with a clear physical interpretation. In an important class of examples, the fermionic form of the formula has a mathematical categorification involving PBW bases for a Cohomological Hall Algebra. The bosonic form lacks an analogous categorification. We construct an equivalence of chain complexes, which categorifies the simplest example of the bosonic wall-crossing formula: the bosonic pentagon identity for the quantum dilogarithm. The chain complexes can be promoted to differential-graded algebras which we relate to the PBW bases of the relevant CoHA by a certain quadratic duality. The equivalence of complexes then follows from the relation between quadratic duality and Koszul duality. We argue that this is a special case of a general phenomenon: the bosonic wall-crossing formulae are categorified to equivalences of \(A_\infty \) algebras which are quadratic dual to PBW presentations of algebras which underlie the fermionic wall-crossing formulae. We give a partial interpretation of our differential-graded algebras in terms of a holomorphic-topological version of BPS webs.
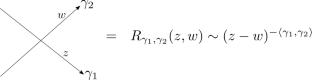

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


