The fiber of persistent homology for trees.

Abstract

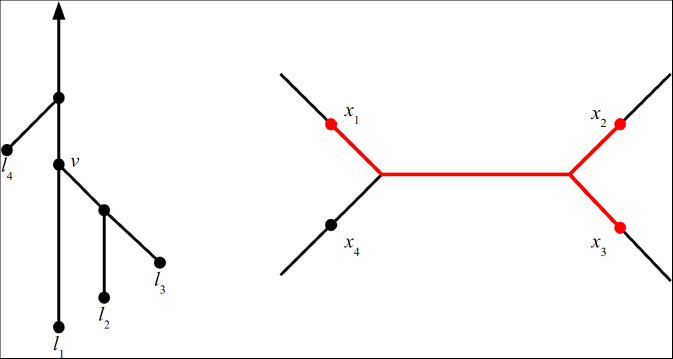
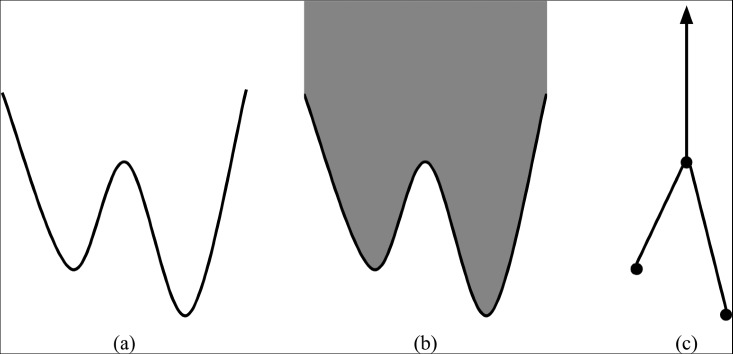
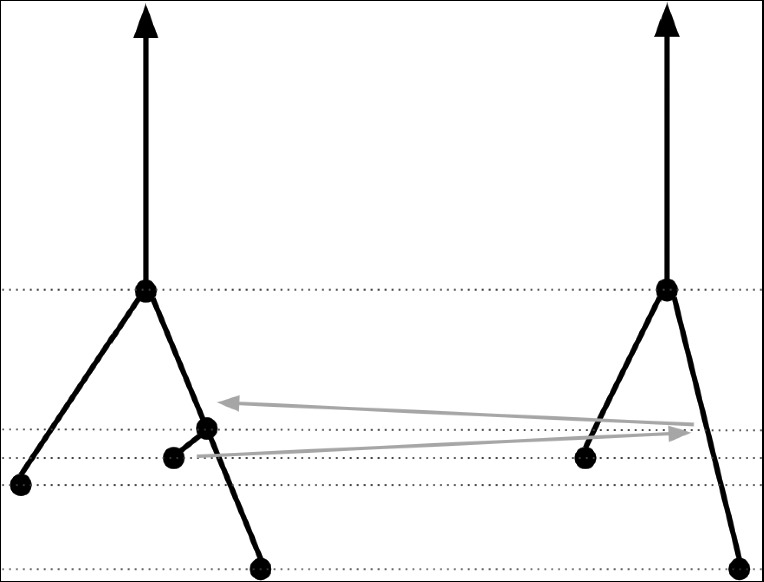
Consider the space of continuous functions on a geometric tree X whose persistent homology gives rise to a finite generic barcode D. We show that there are exactly as many path connected components in this space as there are merge trees whose barcode is D. We find that each component is homotopy equivalent to a configuration space on X with specialised constraints encoded by the merge tree. For barcodes D with either one or two intervals, our method also allows us to compute the homotopy type of this space of functions.