A study of PINN incorporating action principle to predict Landau phase transition

Abstract

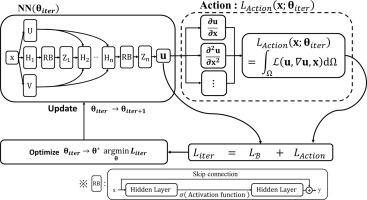
The Landau phase transition materials, making significant configurational changes from subtle perturbation given to the system, have garnered considerable interest because they underpin many engineering applications such as display and semiconductor devices. However, understanding and predicting the transition behavior requires accurate simulation of the complex energetics and finding the energetic minimum, which can only be handled by advanced numerical methods. The recent development of Physics-informed Neural Networks (PINNs), capitalizing on the recent development of deep learning methods and ever-increasing computing power, are deemed promising for revolutionizing numerical simulations as they do not require sophisticated numerical methods but the governing equations describing the system. Nevertheless, the capabilities are significantly limited in predicting phase transition and the dissipative characteristics of the system, which is reported for the first time in the present work. In this study, we present a method predicting relaxed states of the system having phase transitions using a PINN that directly minimizes free energy (Action-PINN) based on the action principle instead of a PINN that searches the equilibrium point of free energy (PDE-PINN). Focusing on the Landau modeling, a general free energy model accounting for the first-, and the second-order phase transition, we first demonstrate that the standard PINN is unable to predict the phase transition and leads only to degenerated solutions. We also demonstrate that the proposed variant of PINN can predict more complex phase transition behavior exhibited by liquid crystals in both 2D and 3D. Moreover, we underscore the model’s efficiency and potential for broader applicability through representative numerical examples. Specifically, we demonstrate enhancing solution fidelity through transfer learning, accurate predictions in heterogeneous systems, and end-to-end optimization.This work offers a significant advancement in extending the utility of PINNs for materials having complex behavior, paving the way for future research and applications for Landau phase transition materials.