PSAFE: A semi-analytical finite element formulation for spatially periodic structural systems

Abstract

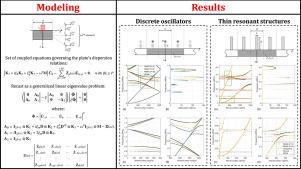
In this article, we present a semi-analytical finite element (SAFE) scheme that enables modeling spatially periodic structural systems. This represents a fundamental extension of the existing SAFE methods, which strictly require translational invariance along the wave propagation direction. Specifically, we develop a formulation that considers viscoelastic plates equipped with regularly spaced resonant structures under plane-strain conditions. Our approach involves (i) imposing Bloch conditions on the unknown displacement field within the plate, (ii) discretizing only the plate’s cross-section, and (iii) modeling the resonant structures as periodic mechanical impedances. This effectively transforms the problem into Fourier space, where the geometrical coordinates are replaced by their Fourier series expansion counterparts. As a result, we obtain an infinite set of coupled equations governing the plate’s dispersion relations, each of which corresponding to a specific Fourier coefficient and containing an infinite number of terms associated with the periodic resonant structures. To solve this problem numerically, we truncate the infinite series to a finite number of terms and then recast the system into a linearized eigenvalue problem. By means of two case studies, we show that accurate results can be achieved even with low truncation orders, and that the accuracy can be refined by increasing the system’s dimensionality, though at the cost of higher computational expense.