Understanding the role of autoencoders for stiff dynamical systems using information theory

Abstract

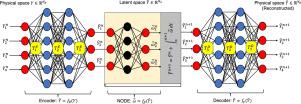
Using information theory, this study provides insights into how the construction of latent space of autoencoder (AE) using deep neural network (DNN) training finds a smooth (non-stiff) low-dimensional manifold in the stiff dynamical system. Our recent study (Vijayarangan et al. 2023) reported that an AE combined with neural ODE (NODE) as a surrogate reduced order model (ROM) for the integration of stiff chemically reacting systems led to a significant reduction in the temporal stiffness, and the behavior was attributed to the identification of a slow invariant manifold by the nonlinear projection using the AE. The present work offers a fundamental understanding of the mechanism of formation of a non-stiff latent space and stiffness reduction by employing concepts from information theory and better mixing. The learning mechanisms of both the encoder and the decoder are explained by plotting the evolution of mutual information and identifying two different phases. Subsequently, the density distribution is plotted for the physical and latent variables, which shows the transformation of the rare event in the physical space to a highly likely (more probable) event in the latent space provided by the nonlinear autoencoder. Finally, the nonlinear transformation leading to density redistribution is explained using concepts from information theory and probability.