Numerical analysis on the effect of obstacles in the mixing dynamics of a supersonic natural gas jet

IF 2.9 3区数学 Q1 MATHEMATICS, APPLIED

Physica D: Nonlinear Phenomena Pub Date : 2025-07-27 DOI:10.1016/j.physd.2025.134840

Ignacio Zamudio-Fernández, Martín Salinas-Vázquez, William Vicente

{"title":"Numerical analysis on the effect of obstacles in the mixing dynamics of a supersonic natural gas jet","authors":"Ignacio Zamudio-Fernández, Martín Salinas-Vázquez, William Vicente","doi":"10.1016/j.physd.2025.134840","DOIUrl":null,"url":null,"abstract":"<div><div>The mixing dynamics of a supersonic natural gas jet in different tubes was investigated numerically using Large Eddy Simulation (LES). The three-dimensional geometries of eight tubes were evaluated to compare pressure, mass fraction, and velocity field evolution; a straight cylindrical tube serves as the reference case. Two cases feature tubes narrowing towards the outlet (one with 2.2 degrees of inclination and another with 3.7 degrees of inclination), and five other cases with 2.2 degrees of inclination and one, two, three, four, or six obstacles added—which decrease the tube diameter. The code employed in this study was validated against three jet cases, showing good agreement with experimental and numerical data. Turbulent regions coincided with regions of maximum natural gas mass fraction. As the number of obstacles increases in each case, mixing enhancement, turbulent regions and pressure gains were higher. The cases with the most obstacles were found to be the ones that had the best mixing enhancement as well as the greatest pressure gains along the length of the tube. The best performing case had an increase in natural gas mass fraction of 13% and in pressure gains of 5% with respect to the reference case, as well as a faster advancement of natural gas. Obstacles too close to the nozzle reduced natural gas advancement and velocity.</div></div>","PeriodicalId":20050,"journal":{"name":"Physica D: Nonlinear Phenomena","volume":"481 ","pages":"Article 134840"},"PeriodicalIF":2.9000,"publicationDate":"2025-07-27","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Physica D: Nonlinear Phenomena","FirstCategoryId":"100","ListUrlMain":"https://www.sciencedirect.com/science/article/pii/S0167278925003173","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS, APPLIED","Score":null,"Total":0}

引用次数: 0

Abstract

The mixing dynamics of a supersonic natural gas jet in different tubes was investigated numerically using Large Eddy Simulation (LES). The three-dimensional geometries of eight tubes were evaluated to compare pressure, mass fraction, and velocity field evolution; a straight cylindrical tube serves as the reference case. Two cases feature tubes narrowing towards the outlet (one with 2.2 degrees of inclination and another with 3.7 degrees of inclination), and five other cases with 2.2 degrees of inclination and one, two, three, four, or six obstacles added—which decrease the tube diameter. The code employed in this study was validated against three jet cases, showing good agreement with experimental and numerical data. Turbulent regions coincided with regions of maximum natural gas mass fraction. As the number of obstacles increases in each case, mixing enhancement, turbulent regions and pressure gains were higher. The cases with the most obstacles were found to be the ones that had the best mixing enhancement as well as the greatest pressure gains along the length of the tube. The best performing case had an increase in natural gas mass fraction of 13% and in pressure gains of 5% with respect to the reference case, as well as a faster advancement of natural gas. Obstacles too close to the nozzle reduced natural gas advancement and velocity.

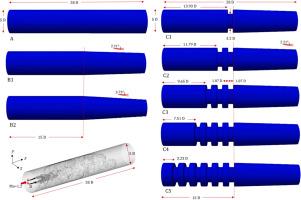
Abstract Image

查看原文本刊更多论文

障碍物对超声速天然气射流混合动力学影响的数值分析

采用大涡模拟方法对超声速天然气射流在不同管道中的混合动力学进行了数值研究。评估了八根管的三维几何形状，比较了压力、质量分数和速度场的演变；一个直的圆柱形管作为参考情况。两种情况下，管道向出口变窄（一种倾斜度为2.2度，另一种倾斜度为3.7度），另外五种情况下，倾斜度为2.2度，并增加了一个、两个、三个、四个或六个障碍物，从而减小了管道直径。本文所采用的代码在三种喷气机情况下进行了验证，与实验和数值数据吻合良好。湍流区与最大天然气质量分数区重合。在每种情况下，随着障碍物数量的增加，混合增强、湍流区域和压力增益都更高。发现障碍最多的情况下，混合增强效果最好，沿管长方向的压力增益最大。与参考情况相比，表现最好的情况下，天然气质量分数增加了13%，压力增加了5%，天然气的推进速度也更快。离喷嘴太近的障碍物降低了天然气的推进和速度。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Physica D: Nonlinear Phenomena 物理-物理：数学物理

CiteScore

7.30

自引率

7.50%

发文量

213

审稿时长

65 days

期刊介绍： Physica D (Nonlinear Phenomena) publishes research and review articles reporting on experimental and theoretical works, techniques and ideas that advance the understanding of nonlinear phenomena. Topics encompass wave motion in physical, chemical and biological systems; physical or biological phenomena governed by nonlinear field equations, including hydrodynamics and turbulence; pattern formation and cooperative phenomena; instability, bifurcations, chaos, and space-time disorder; integrable/Hamiltonian systems; asymptotic analysis and, more generally, mathematical methods for nonlinear systems.