Geometrically Morphological Theory in predictions of dendritic shapes with six-fold crystalline symmetry

Abstract

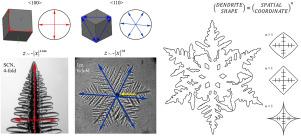
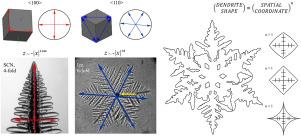
Motivated by important applications in materials physics, we study the shape of dendritic crystals with six-fold crystalline symmetry grown in aqueous solutions of various substances and pure water. Based on recently developed Geometrically Morphological Theory [Philos. Trans. R. Soc. A 378 (2020) 20190243; Phys. Lett. A 501 (2024) 129375] we demonstrate that the shape of the main stem and internal/external envelope in the secondary branches of dendrite at the steady-state growth mode is described by the scaling law $z\left(x\right)\propto -|x{|}^n$ with the values of exponent $n=3.0$ and $n=1.0$ for ice dendrites growing in solutions of Secale cereale, glucose, sucrose and pure water. In addition, by changing the crystalline symmetry from six- to four-fold, the scaling law exponent and the crystallographic growth direction change from $n=1.0$ to $n=1.164$ and $<110>$ to $<100>$, respectively. The evolutionary route of how dendrites reach steady-state growth velocity is also described by supporting and finding parameters from laboratory experiments.