Khovanov Laplacian and Khovanov Dirac for knots and links.
IF 2.6
Q1 MATHEMATICS, INTERDISCIPLINARY APPLICATIONS
Journal of Physics Complexity
Pub Date : 2025-06-01
Epub Date: 2025-06-12
DOI:10.1088/2632-072X/adde9f
引用次数: 0
Abstract
Khovanov homology has been the subject of much study in knot theory and low dimensional topology since 2000. This work introduces a Khovanov Laplacian and a Khovanov Dirac to study knot and link diagrams. The harmonic spectrum of the Khovanov Laplacian or the Khovanov Dirac retains the topological invariants of Khovanov homology, while their non-harmonic spectra reveal additional information that is distinct from Khovanov homology.
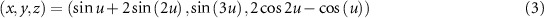
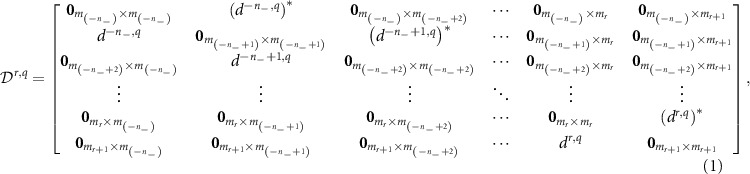
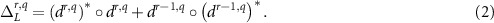
Khovanov Laplacian和Khovanov Dirac。
自2000年以来,Khovanov同调一直是结理论和低维拓扑学研究的主题。本文介绍了一个Khovanov Laplacian和一个Khovanov Dirac来研究结图和连接图。Khovanov拉普拉斯算子和Khovanov狄拉克算子的调和谱保留了Khovanov同调的拓扑不变量,而它们的非调和谱揭示了与Khovanov同调不同的附加信息。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Physics Complexity
Computer Science-Information Systems
CiteScore
4.30
自引率
11.10%
发文量
45
审稿时长
14 weeks
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


