Prethermalization for Deformed Wigner Matrices.

Abstract

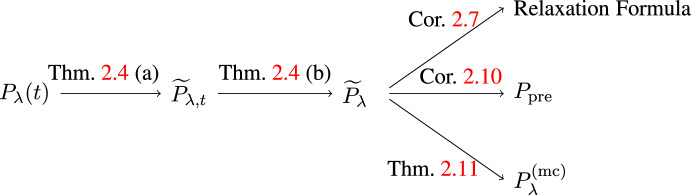
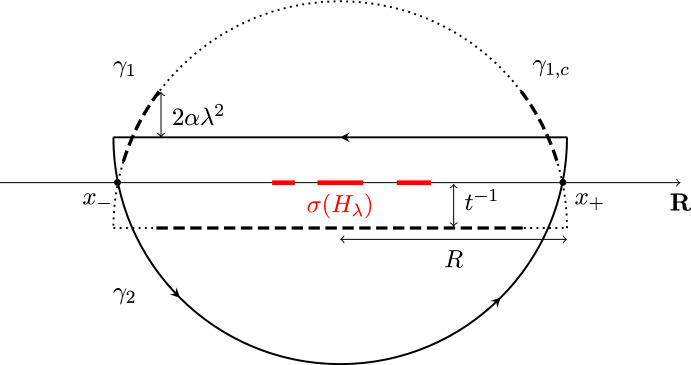
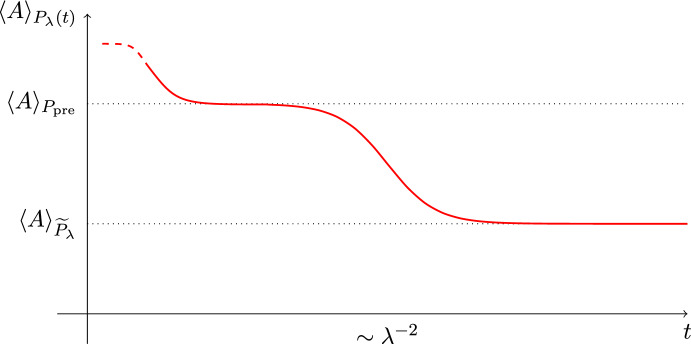
We prove that a class of weakly perturbed Hamiltonians of the form $H_{\lambda }=H_0+\lambda W$ , with W being a Wigner matrix, exhibits prethermalization. That is, the time evolution generated by $H_{\lambda }$ relaxes to its ultimate thermal state via an intermediate prethermal state with a lifetime of order ${\lambda }^{-2}$ . Moreover, we obtain a general relaxation formula, expressing the perturbed dynamics via the unperturbed dynamics and the ultimate thermal state. The proof relies on a two-resolvent law for the deformed Wigner matrix $H_{\lambda }$ .