Adaptive Interface-PINNs (AdaI-PINNs) for inverse problems: Determining material properties for heterogeneous systems
IF 3.5
3区 工程技术
Q1 MATHEMATICS, APPLIED
引用次数: 0
Abstract
We determine spatially varying discontinuous material properties using a domain-decomposition based physics-informed neural networks (PINNs) framework named the Adaptive Interface-PINNs or AdaI-PINNs (Roy et al., 2024). We propose the use of distinct neural networks for the field variables and material properties within each material, utilizing adaptive activation functions. While the neural networks across different materials share the same weights and biases, their activation functions are uniquely tailored using a hyperparameter that influences the slope of the activation function. The proposed framework is tested on several one-dimensional and two-dimensional benchmark examples, and its performance is compared with conventional PINNs and existing domain-decomposition PINNs frameworks, namely, the Multi-domain physics-informed neural network (M-PINN), and the eXtended physics-informed neural networks (XPINNs). The results demonstrate that the proposed approach can determine randomly distributed discontinuous material properties with an error of for the material property and the root-mean-square error of for the primary variable while the other approaches yield errors that are approximately two orders of magnitude larger (that is, ). Moreover, the spatial distribution of material properties obtained using the proposed framework is in close agreement with the true distribution, whereas the other approaches fare much worse. Additionally, the proposed approach is approximately 40% faster than its competitors, indicating its potential as a robust alternative for solving inverse problems in heterogeneous materials.
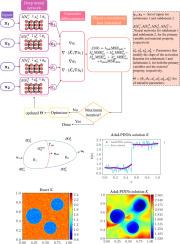
逆问题的自适应接口- pinn (adai - pinn):确定异质系统的材料特性
我们使用基于区域分解的物理信息神经网络(pinn)框架来确定空间变化的不连续材料属性,该框架名为自适应接口- pinn或adai - pinn (Roy等人,2024)。我们建议利用自适应激活函数,对每种材料中的场变量和材料属性使用不同的神经网络。虽然跨不同材料的神经网络共享相同的权重和偏差,但它们的激活函数是使用影响激活函数斜率的超参数进行独特定制的。在多个一维和二维基准示例上对该框架进行了测试,并将其性能与传统pinn和现有的多域物理信息神经网络(M-PINN)和扩展物理信息神经网络(xpinn)进行了比较。结果表明,所提出的方法可以确定随机分布的不连续材料性质,材料性质的L2误差为0(10−3),主变量的均方根误差为0(10−3),而其他方法产生的误差大约大两个数量级(即0(10−1))。此外,使用所提出的框架获得的材料属性的空间分布与真实分布非常接近,而其他方法则差得多。此外,所提出的方法比其竞争对手快大约40%,这表明它有潜力成为解决非均质材料逆问题的强大替代方案。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
4.80
自引率
3.20%
发文量
92
审稿时长
27 days
期刊介绍:
The aim of this journal is to provide ideas and information involving the use of the finite element method and its variants, both in scientific inquiry and in professional practice. The scope is intentionally broad, encompassing use of the finite element method in engineering as well as the pure and applied sciences. The emphasis of the journal will be the development and use of numerical procedures to solve practical problems, although contributions relating to the mathematical and theoretical foundations and computer implementation of numerical methods are likewise welcomed. Review articles presenting unbiased and comprehensive reviews of state-of-the-art topics will also be accommodated.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


