Detail-preserving shape completion of point cloud models with articulated structure
IF 1.7
4区 计算机科学
Q3 COMPUTER SCIENCE, SOFTWARE ENGINEERING
引用次数: 0
Abstract
This paper advocates a novel deep-learning-based method for point cloud completion of multi-categorical articulated objects sharing the same topology. One popular approach for point cloud completion is to rely on a generic encoder-decoder architecture, where the feature maps of input are extracted with the critical set, which essentially consists of a set of points that play critical roles in the max-pooled features. But this pipeline has difficulties in retaining the local details, especially for arbitrary deformable, articulated objects of various categories, bringing category confused completion. In this paper, we propose a detail-preserving point cloud completion method for the complex articulated models by extracting features guided by their articulation topology with a fixed-order scheme, so as to accommodate both fine-grained categorical appearance and non-rigid deformation. First, we construct key subsets, which preserve both local, category-aware and global, non-rigid deformation features simultaneously for input sharing similar point densities, guided by a set of regressed key points approximating articulations. Second, we organize the key subsets with a fixed-order scheme during feature extraction to combat the possible interference due to diverse data component permutations during feature extraction, while upholding the algorithmic efficiency. Finally, we confirm in our evaluations that the new method completes general articulated point clouds with detailed categorical characteristics in high quality. We also show that after training on synthetic data, our method can be applied to real scan or web downloaded point clouds with similar point densities. Meanwhile, we built an Quadruped Point Cloud Completion (QPCC) dataset upon which new research topics could be further explored in geometry modeling and computer graphics.
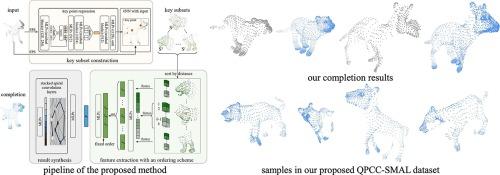
具有关节结构的点云模型的保细节形状补全
本文提出了一种基于深度学习的点云补全新方法,该方法适用于具有相同拓扑结构的多分类铰接对象。点云补全的一种流行方法是依赖于通用的编码器-解码器架构,其中输入的特征映射是用关键集提取的,关键集本质上由一组在最大池特征中起关键作用的点组成。但是,这种管道在保留局部细节方面存在困难,特别是对于任意可变形的、铰接的各种类别的对象,导致类别完成混乱。在本文中,我们提出了一种保留细节的点云补全方法,该方法通过固定顺序的格式提取复杂铰接模型的铰接拓扑引导下的特征,以适应细粒度的分类外观和非刚性变形。首先,在一组近似关节的回归关键点的指导下,我们构建了键子集,该子集同时保留了具有相似点密度的输入的局部、类别感知和全局非刚性变形特征。其次,在特征提取过程中对关键子集进行定序组织,在保证算法效率的前提下,克服了特征提取过程中由于数据成分排列不同而可能产生的干扰。最后,我们在评估中证实,新方法高质量地完成了具有详细分类特征的一般铰接点云。我们还表明,经过对合成数据的训练,我们的方法可以应用于具有相似点密度的真实扫描或网络下载点云。同时,我们建立了一个四足点云补全(QPCC)数据集,在此基础上进一步探索几何建模和计算机图形学的新研究课题。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Computer Aided Geometric Design
工程技术-计算机:软件工程
CiteScore
3.50
自引率
13.30%
发文量
57
审稿时长
60 days
期刊介绍:
The journal Computer Aided Geometric Design is for researchers, scholars, and software developers dealing with mathematical and computational methods for the description of geometric objects as they arise in areas ranging from CAD/CAM to robotics and scientific visualization. The journal publishes original research papers, survey papers and with quick editorial decisions short communications of at most 3 pages. The primary objects of interest are curves, surfaces, and volumes such as splines (NURBS), meshes, subdivision surfaces as well as algorithms to generate, analyze, and manipulate them. This journal will report on new developments in CAGD and its applications, including but not restricted to the following:
-Mathematical and Geometric Foundations-
Curve, Surface, and Volume generation-
CAGD applications in Numerical Analysis, Computational Geometry, Computer Graphics, or Computer Vision-
Industrial, medical, and scientific applications.
The aim is to collect and disseminate information on computer aided design in one journal. To provide the user community with methods and algorithms for representing curves and surfaces. To illustrate computer aided geometric design by means of interesting applications. To combine curve and surface methods with computer graphics. To explain scientific phenomena by means of computer graphics. To concentrate on the interaction between theory and application. To expose unsolved problems of the practice. To develop new methods in computer aided geometry.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


