LatentPINNs: Generative physics-informed neural networks via a latent representation learning

Abstract

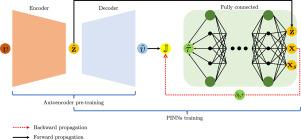
Physics-informed neural networks (PINNs) are promising to replace conventional mesh-based partial differential equation (PDE) solvers by offering more accurate and flexible PDE solutions. However, PINNs are hampered by the relatively slow convergence and the need to perform additional, potentially expensive training for new PDE parameters. To solve this limitation, we introduce LatentPINN, a framework that utilizes latent representations of the PDE parameters as additional (to the coordinates) inputs into PINNs and allows for training over the distribution of these parameters. Motivated by the recent progress on generative models, we promote using latent diffusion models to learn compressed latent representations of the distribution of PDE parameters as they act as input parameters for NN functional solutions. We use a two-stage training scheme in which, in the first stage, we learn the latent representations for the distribution of PDE parameters. In the second stage, we train a physics-informed neural network over inputs given by randomly drawn samples from the coordinate space within the solution domain and samples from the learned latent representation of the PDE parameters. Considering their importance in capturing evolving interfaces and fronts in various fields, we test the approach on a class of level set equations given, for example, by the nonlinear Eikonal equation. We share results corresponding to three Eikonal parameters (velocity models) sets. The proposed method performs well on new phase velocity models without the need for any additional training.