Free-energy machine for combinatorial optimization
IF 18.3
Q1 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS
引用次数: 0
Abstract
Finding optimal solutions to combinatorial optimization problems (COPs) is pivotal in both scientific and industrial domains. Considerable efforts have been invested on developing accelerated methods utilizing sophisticated models and advanced computational hardware. However, the challenge remains to achieve both high efficiency and broad generality in problem-solving. Here we propose a general method, free-energy machine (FEM), based on the ideas of free-energy minimization in statistical physics, combined with automatic differentiation and gradient-based optimization in machine learning. FEM flexibly addresses various COPs within a unified framework and efficiently leverages parallel computational devices such as graphics processing units. We benchmark FEM on diverse COPs including maximum cut, balanced minimum cut and maximum k-satisfiability, scaled to millions of variables, across synthetic and real-world instances. The findings indicate that FEM remarkably outperforms state-of-the-art algorithms tailored for individual COP in both efficiency and efficacy, demonstrating the potential of combining statistical physics and machine learning for broad applications. This work introduces the free-energy machine (FEM), which combines statistical physics principles and machine learning techniques to solve various combinatorial optimization problems. FEM outperforms state-of-the-art algorithms in both efficiency and effectiveness across multiple combinatorial optimization problems, demonstrating its broad applicability.
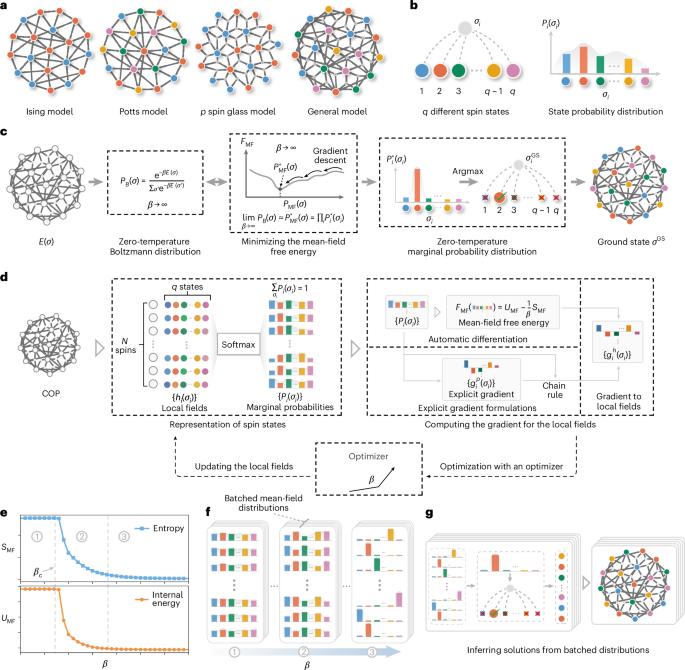
组合优化的自由能机。
寻找组合优化问题的最优解在科学和工业领域都是至关重要的。在利用复杂的模型和先进的计算硬件开发加速方法方面投入了相当大的努力。然而,在解决问题方面实现高效率和广泛的通用性仍然是一项挑战。本文基于统计物理中的自由能最小化思想,结合机器学习中的自动微分和基于梯度的优化,提出了一种通用的方法——自由能机(FEM)。FEM在统一的框架内灵活地处理各种cop,并有效地利用并行计算设备(如图形处理单元)。我们在各种cop上对FEM进行基准测试,包括最大切割,平衡最小切割和最大k-可满足性,在合成和现实世界的实例中缩放到数百万个变量。研究结果表明,FEM在效率和功效方面都明显优于为单个COP量身定制的最先进算法,这表明了将统计物理和机器学习结合起来进行广泛应用的潜力。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


