Quadratic Euler characteristic of symmetric powers of curves.
IF 0.6
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
We compute the quadratic Euler characteristic of the symmetric powers of a smooth, projective curve over any field k that is not of characteristic two, using the Motivic Gauss-Bonnet Theorem of Levine-Raksit. As an application, we show that the power structure on the Grothendieck-Witt ring introduced by Pajwani-Pál computes the compactly supported -Euler characteristic of symmetric powers for all curves.
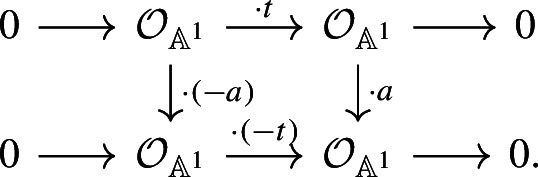
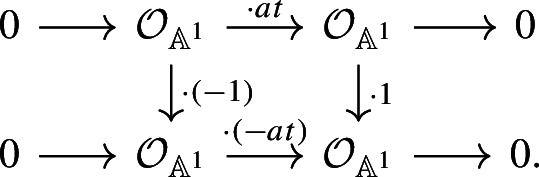
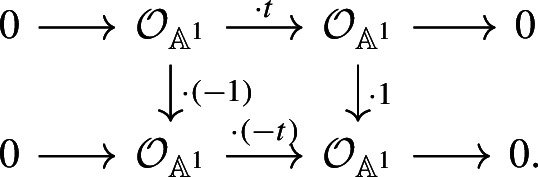
曲线对称幂的二次欧拉特性。
我们利用Levine-Raksit的动机高斯-博内定理,计算了任意场k上不具有特征二的光滑投影曲线的对称幂的二次欧拉特征。作为一个应用,我们证明了Pajwani-Pál引入的Grothendieck-Witt环上的幂结构计算了所有曲线对称幂的紧支A 1 -欧拉特性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Manuscripta Mathematica
数学-数学
CiteScore
1.40
自引率
0.00%
发文量
86
审稿时长
6-12 weeks
期刊介绍:
manuscripta mathematica was founded in 1969 to provide a forum for the rapid communication of advances in mathematical research. Edited by an international board whose members represent a wide spectrum of research interests, manuscripta mathematica is now recognized as a leading source of information on the latest mathematical results.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


