Loschmidt echo for deformed Wigner matrices

Abstract

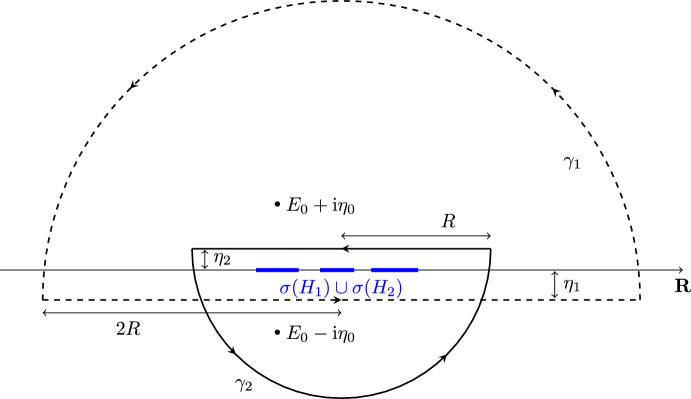
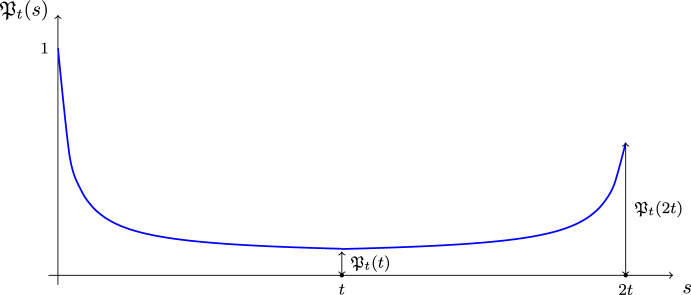
We consider two Hamiltonians that are close to each other, \(H_1 \approx H_2 \), and analyze the time decay of the corresponding Loschmidt echo \(\mathfrak {M}(t):= |\langle \psi _0, \textrm{e}^{\textrm{i} t H_2} \textrm{e}^{-\textrm{i} t H_1} \psi _0 \rangle |^2\) that expresses the effect of an imperfect time reversal on the initial state \(\psi _0\). Our model Hamiltonians are deformed Wigner matrices that do not share a common eigenbasis. The main tools are new two-resolvent laws for such \(H_1\) and \(H_2\).