Subintuitionistic logics and their modal companions: a nested approach.
Q1 Arts and Humanities
Journal of Applied Non-Classical Logics
Pub Date : 2024-08-03
eCollection Date: 2024-01-01
DOI:10.1080/11663081.2024.2366756
引用次数: 0
Abstract
In the present paper we deal with subintuitionistic logics and their modal companions. In particular, we introduce nested calculi for subintuitionistic systems and for modal logics in the modal cube ranging from to . The latter calculi differ from standard nested systems, as there are multiple rules handling the modal operator. As an upshot, we get a purely syntactic proof of the Gödel-McKinsey-Tarski embedding which preserves the structure and the height of the derivations. Finally, we obtain a conservativity result for classical logic over a weak subintuitionistic system.
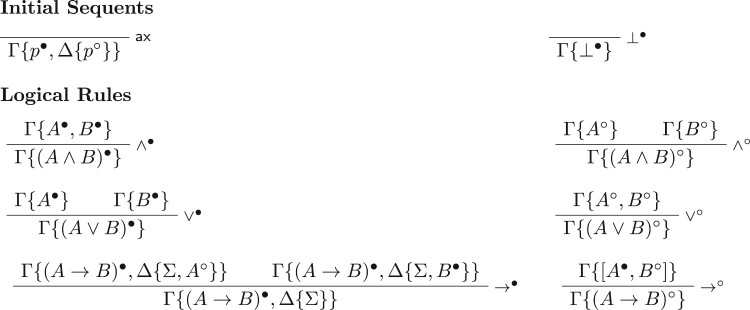
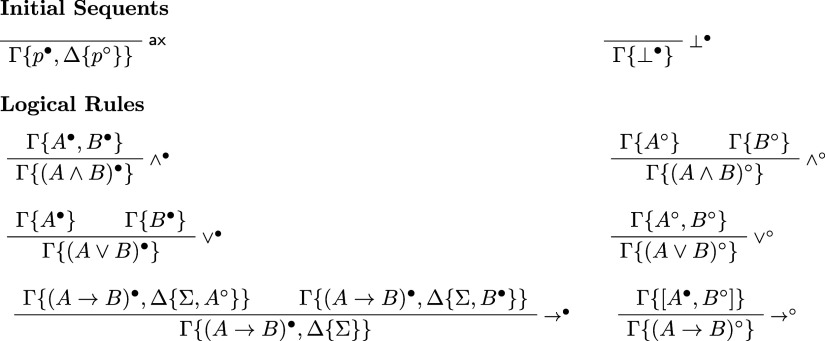
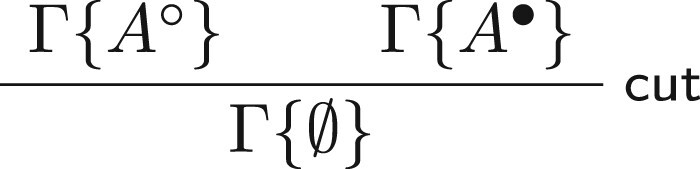
次直觉逻辑及其模态同伴:一种嵌套方法。
在本文中,我们讨论了次直觉逻辑及其模态同伴。特别地,我们在S 5模态立方K到S 4范围内引入了子直觉系统和模态逻辑的嵌套演算。后一种演算不同于标准的嵌套系统,因为有多个规则处理模态操作符。作为结果,我们得到了Gödel-McKinsey-Tarski嵌入的纯语法证明,它保留了衍生的结构和高度。最后,我们得到了经典逻辑在弱次直觉系统上的保守性结果。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Applied Non-Classical Logics
Arts and Humanities-Philosophy
CiteScore
1.30
自引率
0.00%
发文量
8
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


