A Study of Fractional Order Financial Crime Model Using the Gegenbauer Wavelet Collocation Method
IF 2.9
4区 工程技术
Q1 MULTIDISCIPLINARY SCIENCES
引用次数: 0
Abstract
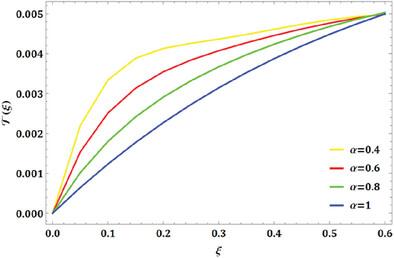
The manuscript investigates the numerical approximation of the fractional mathematical model of the financial crime population dynamics by the Gegenbauer wavelet collocation method. The study aims to enhance the accuracy and efficiency of solving the underlying differential equations that describe these phenomena by utilizing the proposed technique. The financial crime model is a nonlinear coupled system of ordinary differential equations. Using the Gegenbauer wavelets, the novel operational matrices of integration are created. A nonlinear system of ordinary differential equations are transformed into a system of algebraic equations using the characteristics of the Gegenbauer wavelet expansions and the operational matrix of integration, which speeds up processing. Then, this system of algebraic equations is solved using the Newton-iterative technique to find the unknown Gegenbauer coefficients that help to obtain the approximate solution for the system. A numerical illustration is presented to show the efficacy and precision of the approach. The numerical results obtained from the projected approach are compared with the existing methods, such as NDSolve and Runge Kutta methods. These results show that the projected scheme is simple, reliable, and resilient. The findings suggest that this approach can be a powerful tool for researchers and practitioners in the financial sector, aiding in developing crime prevention and intervention strategies. The study concludes with suggestions for future research directions.
使用格根鲍尔小波配位法的分数阶金融犯罪模型研究
本文研究了基于Gegenbauer小波搭配法的金融犯罪人口动态分数数学模型的数值逼近。本研究旨在利用所提出的技术,提高求解描述这些现象的潜在微分方程的准确性和效率。金融犯罪模型是一个常微分方程的非线性耦合系统。利用Gegenbauer小波,建立了新的积分运算矩阵。利用Gegenbauer小波展开式和积分运算矩阵的特点,将非线性常微分方程组转化为代数方程组,提高了处理速度。然后,利用牛顿迭代法求解该代数方程组,求出未知的Gegenbauer系数,从而得到系统的近似解。算例表明了该方法的有效性和准确性。将投影法得到的数值结果与现有的NDSolve法和Runge Kutta法进行了比较。结果表明,该方案简单、可靠,具有较强的弹性。研究结果表明,这种方法可以成为金融部门研究人员和从业人员的有力工具,有助于制定预防犯罪和干预战略。最后,对今后的研究方向提出了建议。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Advanced Theory and Simulations
Multidisciplinary-Multidisciplinary
CiteScore
5.50
自引率
3.00%
发文量
221
期刊介绍:
Advanced Theory and Simulations is an interdisciplinary, international, English-language journal that publishes high-quality scientific results focusing on the development and application of theoretical methods, modeling and simulation approaches in all natural science and medicine areas, including:
materials, chemistry, condensed matter physics
engineering, energy
life science, biology, medicine
atmospheric/environmental science, climate science
planetary science, astronomy, cosmology
method development, numerical methods, statistics
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


