Tolman Length for Binary Polymer–Polymer and Polymer–Solvent Systems

IF 5.2 1区化学 Q1 POLYMER SCIENCE

Macromolecules Pub Date : 2024-12-04 DOI:10.1021/acs.macromol.4c02073

F. A. M. Leermakers

引用次数: 0

Abstract

The liquid–liquid interface continues to be at the focus of scientific research for many good reasons. Even though the first theoretical results by van der Waals are known for over a century, there are still relevant issues to address. We present numerical self-consistent field results for both binary polymer A_NA/B_NB- and polymer–solvent A_{N_A}/B₁ systems and found that the Tolman length δ invariably vanishes at strong segregation, and remains smaller than the segment size when N_A ≈ N_B. However, for polymer–solvent systems in the weak segregation limit δ approaches a limiting value proportional to the radius of gyration of the polymer, that is when the interfacial width is larger that the coil size(s). It is argued that for a two-phase polymer–solvent systems, mesoscale solvent droplets may develop and exist (for long times) in the polymer rich phase, offering an explanation for its cloudy appearance.

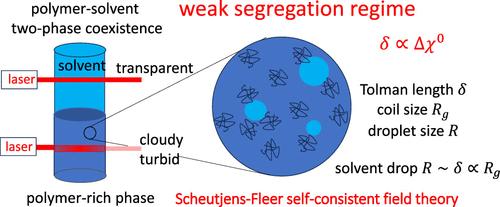
Abstract Image

查看原文本刊更多论文

二元聚合物-聚合物和聚合物-溶剂体系的托尔曼长度

液-液界面一直是科学研究的焦点，原因有很多。尽管范德瓦尔斯的第一个理论结果已经被知道了一个多世纪，但仍然有相关的问题需要解决。我们给出了二元聚合物ANA/BNB-和聚合物溶剂ANA/B1体系的数值自一致场结果，发现托尔曼长度δ总是在强偏析下消失，并且在NA≈NB时仍然小于段尺寸。然而，对于弱偏析的聚合物-溶剂体系，当界面宽度大于线圈尺寸(s)时，δ接近与聚合物旋转半径成正比的极限值。本文认为，对于两相聚合物-溶剂体系，中尺度溶剂液滴可能在富聚合物相中发育并长期存在，这解释了其浑浊现象。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Macromolecules 工程技术-高分子科学

CiteScore

9.30

自引率

16.40%

发文量

942

审稿时长

2 months

期刊介绍： Macromolecules publishes original, fundamental, and impactful research on all aspects of polymer science. Topics of interest include synthesis (e.g., controlled polymerizations, polymerization catalysis, post polymerization modification, new monomer structures and polymer architectures, and polymerization mechanisms/kinetics analysis); phase behavior, thermodynamics, dynamic, and ordering/disordering phenomena (e.g., self-assembly, gelation, crystallization, solution/melt/solid-state characteristics); structure and properties (e.g., mechanical and rheological properties, surface/interfacial characteristics, electronic and transport properties); new state of the art characterization (e.g., spectroscopy, scattering, microscopy, rheology), simulation (e.g., Monte Carlo, molecular dynamics, multi-scale/coarse-grained modeling), and theoretical methods. Renewable/sustainable polymers, polymer networks, responsive polymers, electro-, magneto- and opto-active macromolecules, inorganic polymers, charge-transporting polymers (ion-containing, semiconducting, and conducting), nanostructured polymers, and polymer composites are also of interest. Typical papers published in Macromolecules showcase important and innovative concepts, experimental methods/observations, and theoretical/computational approaches that demonstrate a fundamental advance in the understanding of polymers.