Mengzhu Shi, Kaibao Fan, Houpu Li, Senyang Pan, Jiaqiang Cai, Nan Zhang, Hongyu Li, Tao Wu, Jinglei Zhang, Chuanying Xi, Ziji Xiang, Xianhui Chen
求助PDF
{"title":"Two-Dimensional Superconductivity and Anomalous Vortex Dissipation in Newly Discovered Transition Metal Dichalcogenide-Based Superlattices","authors":"Mengzhu Shi, Kaibao Fan, Houpu Li, Senyang Pan, Jiaqiang Cai, Nan Zhang, Hongyu Li, Tao Wu, Jinglei Zhang, Chuanying Xi, Ziji Xiang, Xianhui Chen","doi":"10.1021/jacs.4c09248","DOIUrl":null,"url":null,"abstract":"Properties of layered superconductors can vary drastically when thinned down from bulk to monolayer owing to the reduced dimensionality and weakened interlayer coupling. In transition metal dichalcogenides (TMDs), the inherent symmetry breaking effect in atomically thin crystals prompts novel states of matter such as Ising superconductivity with an extraordinary in-plane upper critical field. Here, we demonstrate that two-dimensional (2D) superconductivity resembling those in atomic layers but with more fascinating behaviors can be realized in the bulk crystals of two new TMD-based superconductors Ba<sub>0.75</sub>ClTaS<sub>2</sub> and Ba<sub>0.75</sub>ClTaSe<sub>2</sub> with superconducting transition temperatures 2.75 and 1.75 K, respectively. They comprise an alternating stack of H-type TMD layers and Ba–Cl layers. In both materials, intrinsic 2D superconductivity develops below a Berezinskii–Kosterlitz–Thouless transition. The upper critical field along <i>the ab</i> plane (<i></i><span style=\"color: inherit;\"></span><span data-mathml='<math xmlns=\"http://www.w3.org/1998/Math/MathML\" display=\"inline\" overflow=\"scroll\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math>' role=\"presentation\" style=\"position: relative;\" tabindex=\"0\"><nobr aria-hidden=\"true\"><span overflow=\"scroll\" style=\"width: 2.446em; display: inline-block;\"><span style=\"display: inline-block; position: relative; width: 2.219em; height: 0px; font-size: 110%;\"><span style=\"position: absolute; clip: rect(1.026em, 1002.22em, 2.673em, -999.997em); top: -2.156em; left: 0em;\"><span><span><span style=\"display: inline-block; position: relative; width: 2.219em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.185em, 1000.91em, 4.151em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝐻<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.06em;\"></span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.298em, 1001.2em, 4.264em, -999.997em); top: -4.429em; left: 0.969em;\"><span><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Variants;\">|</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Variants;\">|</span></span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑎</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑏</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.355em, 1000.74em, 4.151em, -999.997em); top: -3.634em; left: 0.855em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑐</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">2</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span></span><span style=\"display: inline-block; width: 0px; height: 2.162em;\"></span></span></span><span style=\"display: inline-block; overflow: hidden; vertical-align: -0.434em; border-left: 0px solid; width: 0px; height: 1.566em;\"></span></span></nobr><span role=\"presentation\"><math display=\"inline\" overflow=\"scroll\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math></span></span><script type=\"math/mml\"><math display=\"inline\" overflow=\"scroll\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math></script>) exceeds the Pauli limit (<i>μ</i><sub><i>0</i></sub><i>H</i><sub>p</sub>); in particular, Ba<sub>0.75</sub>ClTaSe<sub>2</sub> exhibits an extremely high <i></i><span style=\"color: inherit;\"></span><span data-mathml='<math xmlns=\"http://www.w3.org/1998/Math/MathML\" display=\"inline\" overflow=\"scroll\"><msub><mrow><mi>&#x3BC;</mi></mrow><mrow><mn>0</mn></mrow></msub><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math>' role=\"presentation\" style=\"position: relative;\" tabindex=\"0\"><nobr aria-hidden=\"true\"><span overflow=\"scroll\" style=\"width: 3.582em; display: inline-block;\"><span style=\"display: inline-block; position: relative; width: 3.241em; height: 0px; font-size: 110%;\"><span style=\"position: absolute; clip: rect(1.026em, 1003.24em, 2.673em, -999.997em); top: -2.156em; left: 0em;\"><span><span><span style=\"display: inline-block; position: relative; width: 1.026em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.355em, 1000.57em, 4.321em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝜇</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; top: -3.747em; left: 0.571em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">0</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span><span><span style=\"display: inline-block; position: relative; width: 2.219em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.185em, 1000.91em, 4.151em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝐻<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.06em;\"></span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.298em, 1001.2em, 4.264em, -999.997em); top: -4.429em; left: 0.969em;\"><span><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Variants;\">|</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Variants;\">|</span></span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑎</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑏</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.355em, 1000.74em, 4.151em, -999.997em); top: -3.634em; left: 0.855em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑐</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">2</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span></span><span style=\"display: inline-block; width: 0px; height: 2.162em;\"></span></span></span><span style=\"display: inline-block; overflow: hidden; vertical-align: -0.434em; border-left: 0px solid; width: 0px; height: 1.566em;\"></span></span></nobr><span role=\"presentation\"><math display=\"inline\" overflow=\"scroll\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><msub><mrow><mi>μ</mi></mrow><mrow><mn>0</mn></mrow></msub><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math></span></span><script type=\"math/mml\"><math display=\"inline\" overflow=\"scroll\"><msub><mrow><mi>μ</mi></mrow><mrow><mn>0</mn></mrow></msub><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math></script>≈ 14 <i>μ</i><sub><i>0</i></sub><i>H</i><sub><i>p</i></sub> and a colossal superconducting anisotropy (<i></i><span style=\"color: inherit;\"></span><span data-mathml='<math xmlns=\"http://www.w3.org/1998/Math/MathML\" display=\"inline\" overflow=\"scroll\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math>' role=\"presentation\" style=\"position: relative;\" tabindex=\"0\"><nobr aria-hidden=\"true\"><span overflow=\"scroll\" style=\"width: 2.446em; display: inline-block;\"><span style=\"display: inline-block; position: relative; width: 2.219em; height: 0px; font-size: 110%;\"><span style=\"position: absolute; clip: rect(1.026em, 1002.22em, 2.673em, -999.997em); top: -2.156em; left: 0em;\"><span><span><span style=\"display: inline-block; position: relative; width: 2.219em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.185em, 1000.91em, 4.151em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝐻<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.06em;\"></span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.298em, 1001.2em, 4.264em, -999.997em); top: -4.429em; left: 0.969em;\"><span><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Variants;\">|</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Variants;\">|</span></span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑎</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑏</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.355em, 1000.74em, 4.151em, -999.997em); top: -3.634em; left: 0.855em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑐</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">2</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span></span><span style=\"display: inline-block; width: 0px; height: 2.162em;\"></span></span></span><span style=\"display: inline-block; overflow: hidden; vertical-align: -0.434em; border-left: 0px solid; width: 0px; height: 1.566em;\"></span></span></nobr><span role=\"presentation\"><math display=\"inline\" overflow=\"scroll\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math></span></span><script type=\"math/mml\"><math display=\"inline\" overflow=\"scroll\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mrow><mo stretchy=\"false\">|</mo><mo stretchy=\"false\">|</mo></mrow><mi>a</mi><mi>b</mi></mrow></msubsup></math></script>/<i></i><span style=\"color: inherit;\"></span><span data-mathml='<math xmlns=\"http://www.w3.org/1998/Math/MathML\" display=\"inline\" overflow=\"scroll\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mo lspace=\"0.03em\" rspace=\"0.03em\">&#x22A5;</mo><mi>a</mi><mi>b</mi></mrow></msubsup></math>' role=\"presentation\" style=\"position: relative;\" tabindex=\"0\"><nobr aria-hidden=\"true\"><span overflow=\"scroll\" style=\"width: 2.56em; display: inline-block;\"><span style=\"display: inline-block; position: relative; width: 2.332em; height: 0px; font-size: 110%;\"><span style=\"position: absolute; clip: rect(1.139em, 1002.33em, 2.616em, -999.997em); top: -2.156em; left: 0em;\"><span><span><span style=\"display: inline-block; position: relative; width: 2.332em; height: 0px;\"><span style=\"position: absolute; clip: rect(3.185em, 1000.91em, 4.151em, -999.997em); top: -3.974em; left: 0em;\"><span><span style=\"font-family: STIXMathJax_Normal-italic;\">𝐻<span style=\"display: inline-block; overflow: hidden; height: 1px; width: 0.06em;\"></span></span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.355em, 1001.31em, 4.151em, -999.997em); top: -4.372em; left: 0.969em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main; padding-left: 0.06em; padding-right: 0.06em;\">⊥</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑎</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑏</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span><span style=\"position: absolute; clip: rect(3.355em, 1000.74em, 4.151em, -999.997em); top: -3.69em; left: 0.855em;\"><span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Normal-italic;\">𝑐</span><span style=\"font-size: 70.7%; font-family: STIXMathJax_Main;\">2</span></span><span style=\"display: inline-block; width: 0px; height: 3.98em;\"></span></span></span></span></span><span style=\"display: inline-block; width: 0px; height: 2.162em;\"></span></span></span><span style=\"display: inline-block; overflow: hidden; vertical-align: -0.372em; border-left: 0px solid; width: 0px; height: 1.378em;\"></span></span></nobr><span role=\"presentation\"><math display=\"inline\" overflow=\"scroll\" xmlns=\"http://www.w3.org/1998/Math/MathML\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mo lspace=\"0.03em\" rspace=\"0.03em\">⊥</mo><mi>a</mi><mi>b</mi></mrow></msubsup></math></span></span><script type=\"math/mml\"><math display=\"inline\" overflow=\"scroll\"><msubsup><mrow><mi>H</mi></mrow><mrow><mi>c</mi><mn>2</mn></mrow><mrow><mo lspace=\"0.03em\" rspace=\"0.03em\">⊥</mo><mi>a</mi><mi>b</mi></mrow></msubsup></math></script>) of ∼150. Moreover, the temperature-field phase diagram of Ba<sub>0.75</sub>ClTaSe<sub>2</sub> under an in-plane magnetic field contains a large phase regime of vortex dissipation, which can be ascribed to the Josephson vortex motion, signifying an unprecedentedly strong fluctuation effect in TMD-based superconductors. Our results provide a new path toward the establishment of 2D superconductivity and novel exotic quantum phases in bulk crystals of TMD-based superconductors.","PeriodicalId":49,"journal":{"name":"Journal of the American Chemical Society","volume":"58 1","pages":""},"PeriodicalIF":14.4000,"publicationDate":"2024-11-25","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of the American Chemical Society","FirstCategoryId":"92","ListUrlMain":"https://doi.org/10.1021/jacs.4c09248","RegionNum":1,"RegionCategory":"化学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"CHEMISTRY, MULTIDISCIPLINARY","Score":null,"Total":0}
引用次数: 0
引用
批量引用
Abstract
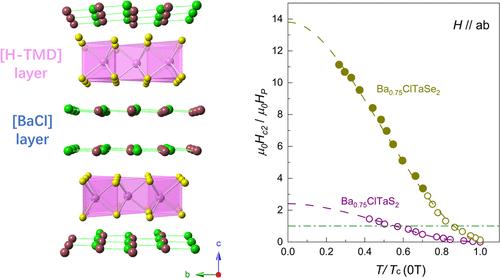
Properties of layered superconductors can vary drastically when thinned down from bulk to monolayer owing to the reduced dimensionality and weakened interlayer coupling. In transition metal dichalcogenides (TMDs), the inherent symmetry breaking effect in atomically thin crystals prompts novel states of matter such as Ising superconductivity with an extraordinary in-plane upper critical field. Here, we demonstrate that two-dimensional (2D) superconductivity resembling those in atomic layers but with more fascinating behaviors can be realized in the bulk crystals of two new TMD-based superconductors Ba
0.75 ClTaS
2 and Ba
0.75 ClTaSe
2 with superconducting transition temperatures 2.75 and 1.75 K, respectively. They comprise an alternating stack of H-type TMD layers and Ba–Cl layers. In both materials, intrinsic 2D superconductivity develops below a Berezinskii–Kosterlitz–Thouless transition. The upper critical field along
the ab plane (
𝐻 | | 𝑎 𝑏 𝑐 2 H c 2 | | a b ) exceeds the Pauli limit (
μ 0 H p ); in particular, Ba
0.75 ClTaSe
2 exhibits an extremely high
𝜇 0 𝐻 | | 𝑎 𝑏 𝑐 2 μ 0 H c 2 | | a b ≈ 14
μ 0 H p and a colossal superconducting anisotropy (
𝐻 | | 𝑎 𝑏 𝑐 2 H c 2 | | a b /
𝐻 ⊥ 𝑎 𝑏 𝑐 2 H c 2 ⊥ a b ) of ∼150. Moreover, the temperature-field phase diagram of Ba
0.75 ClTaSe
2 under an in-plane magnetic field contains a large phase regime of vortex dissipation, which can be ascribed to the Josephson vortex motion, signifying an unprecedentedly strong fluctuation effect in TMD-based superconductors. Our results provide a new path toward the establishment of 2D superconductivity and novel exotic quantum phases in bulk crystals of TMD-based superconductors.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


