A Physics-Driven GraphSAGE Method for Physical Field Simulations Described by Partial Differential Equations

Abstract

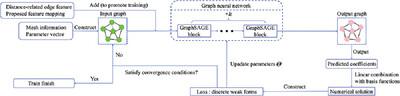
Physics-informed neural networks (PINNs) have successfully addressed various computational physics problems based on partial differential equations (PDEs). However, while tackling issues related to irregularities like singularities and oscillations, trained solutions usually suffer low accuracy. In addition, most current works only offer the trained solution for predetermined input parameters. If any change occurs in input parameters, transfer learning or retraining is required, and traditional numerical techniques also need recomputation. In this work, a physics-driven GraphSAGE approach (PD-GraphSAGE) based on the Galerkin method and piecewise polynomial nodal basis functions is presented to solve computational problems governed by irregular PDEs and to develop parametric PDE surrogate models. This approach employs graph representations of physical domains, thereby reducing the demands for evaluated points due to local refinement. A distance-related edge feature and a feature mapping strategy are devised to help training and convergence for singularity and oscillation situations, respectively. The merits of the proposed method are demonstrated through a couple of cases. Moreover, the robust PDE surrogate model for heat conduction problems parameterized by the Gaussian random field source is successfully established, which not only provides the solution accurately but is several times faster than the finite element method in the experiments.