Optimal one-sided approximants of circular arc

IF 1.3 4区计算机科学 Q3 COMPUTER SCIENCE, SOFTWARE ENGINEERING

Computer Aided Geometric Design Pub Date : 2024-11-12 DOI:10.1016/j.cagd.2024.102401

Ada Šadl Praprotnik , Aleš Vavpetič , Emil Žagar

引用次数: 0

Abstract

The optimal one-sided parametric polynomial approximants of a circular arc are considered. More precisely, the approximant must be entirely in or out of the underlying circle of an arc. The natural restriction to an arc's approximants interpolating boundary points is assumed. However, the study of approximants, which additionally interpolate corresponding tangent directions and curvatures at the boundary of an arc, is also considered. Several low-degree polynomial approximants are studied in detail. When several solutions fulfilling the interpolation conditions exist, the optimal one is characterized, and a numerical algorithm for its construction is suggested. Theoretical results are demonstrated with several numerical examples and a comparison with general (i.e. non-one-sided) approximants are provided.

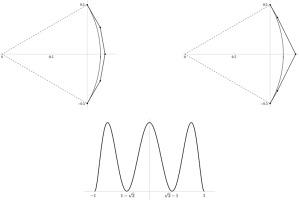
Abstract Image

查看原文本刊更多论文

圆弧的最佳单边近似值

本文考虑了圆弧的最优单边参数多项式近似值。更确切地说，近似值必须完全在弧的底圆之内或之外。弧的近似值插值边界点的自然限制是假定的。然而，我们也考虑了对近似值的研究，这些近似值在弧的边界上插值相应的切线方向和曲率。本文详细研究了几种低度多项式近似值。当存在多个满足插值条件的解时，对最优解进行了表征，并提出了构建最优解的数值算法。通过几个数值实例证明了理论结果，并提供了与一般（即非单边）近似值的比较。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Computer Aided Geometric Design 工程技术-计算机：软件工程

CiteScore

3.50

自引率

13.30%

发文量

审稿时长

60 days

期刊介绍： The journal Computer Aided Geometric Design is for researchers, scholars, and software developers dealing with mathematical and computational methods for the description of geometric objects as they arise in areas ranging from CAD/CAM to robotics and scientific visualization. The journal publishes original research papers, survey papers and with quick editorial decisions short communications of at most 3 pages. The primary objects of interest are curves, surfaces, and volumes such as splines (NURBS), meshes, subdivision surfaces as well as algorithms to generate, analyze, and manipulate them. This journal will report on new developments in CAGD and its applications, including but not restricted to the following: -Mathematical and Geometric Foundations- Curve, Surface, and Volume generation- CAGD applications in Numerical Analysis, Computational Geometry, Computer Graphics, or Computer Vision- Industrial, medical, and scientific applications. The aim is to collect and disseminate information on computer aided design in one journal. To provide the user community with methods and algorithms for representing curves and surfaces. To illustrate computer aided geometric design by means of interesting applications. To combine curve and surface methods with computer graphics. To explain scientific phenomena by means of computer graphics. To concentrate on the interaction between theory and application. To expose unsolved problems of the practice. To develop new methods in computer aided geometry.