How accurate is density functional theory at high pressures?

Abstract

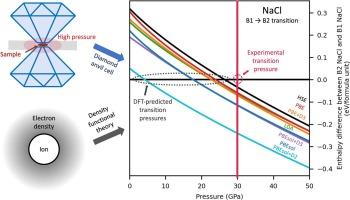
Density functional theory (DFT) is widely used to study the behavior of materials at high pressures, complementing challenging and often costly experiments. While the accuracy of DFT and the effect of various approximations and corrections have been extensively studied for materials properties around ambient conditions, few studies quantified accuracy at high pressures. We focus on the accuracy of predicted equations of state (EOS) of selected materials up to the hundred GPa regime and the description of pressure-induced phase transformations. We characterize the effect of exchange–correlation functionals, pseudopotentials, dispersion and Hubbard U correction and find that lessons-learned at ambient conditions do not always translate into the high-pressure regime. We find that the Perdew-Burke-Erzerhof solid version of the generalized gradient approximation (GGA) yields the best performance in both EOS and transformation pressure compared to Perdew-Burke-Erzerhof version of GGA, local density approximations (LDA), and the Heyd-Scuseria-Ernzerhof (HSE) hybrid functional. Adding dispersion corrections known as D2 and D3 does not improve the results. Interestingly, the local density approximation performed remarkably well. We also find that the Hubbard-U correction as a significant effect on transformation pressures in strongly correlated materials systems, indicating that the U parameter must be chosen carefully. An important by-product of this study is a FAIR repository of high-pressure simulations database on nanoHUB.