Phase field numerical model for simulating the diffusion controlled stress corrosion cracking phenomena in anisotropic material
IF 3.1
3区 材料科学
Q2 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
Abstract
In this study, we develop a phase field numerical model to simulate diffusion-controlled stress corrosion cracking (SCC) in anisotropic materials. Our model is based on multiphysics model involving the electrochemical process, the mechanical response of the material, and the coupling between them. The corrosion system consists of a metallic solid phase immersed in an electrolyte, initially protected by a passive film. The model captures the breakdown of this film, leading to localized pitting corrosion, which subsequently evolves into stress corrosion cracking under the influence of mechanical stress. We employ the Allen-Cahn equation to describe the evolution of the non-conserved phase field variable, representing the metal-electrolyte interface, and the Cahn-Hilliard equation to account for the concentration field dynamics, ensuring volume conservation. The mechanical behavior of the anisotropic material is modeled using crystal plasticity, which accounts for the elastic and plastic deformation of the material, with the degradation due to corrosion incorporated into the stress–strain relationship. We analyze the transition from pitting to cracking in single crystalline, bi-crystalline, and polycrystalline structures. The results demonstrate the capability of the model to capture the complex interactions between electrochemical corrosion and mechanical deformation, providing insights into the pit-to-crack transition in anisotropic materials. The developed phase field numerical model presents a significant advancement in understanding and simulating SCC phenomena, with potential applications in various engineering fields where corrosion is a critical concern.
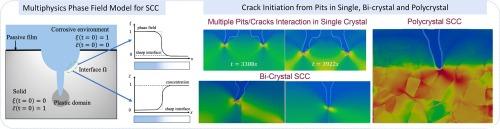
用于模拟各向异性材料中扩散控制应力腐蚀开裂现象的相场数值模型
在本研究中,我们开发了一种相场数值模型,用于模拟各向异性材料中的扩散控制应力腐蚀开裂(SCC)。我们的模型基于多物理场模型,涉及电化学过程、材料的机械响应以及它们之间的耦合。腐蚀系统由浸入电解质中的金属固相组成,最初由一层被动薄膜保护。该模型捕捉了这层膜的破坏过程,从而导致局部点状腐蚀,随后在机械应力的影响下演变为应力腐蚀开裂。我们采用 Allen-Cahn 方程来描述代表金属-电解质界面的非守恒相场变量的演变,并采用 Cahn-Hilliard 方程来解释浓度场动态,以确保体积守恒。各向异性材料的机械行为使用晶体塑性来建模,该模型考虑了材料的弹性和塑性变形,并将腐蚀引起的降解纳入应力应变关系中。我们分析了单晶、双晶和多晶结构中从点蚀到开裂的转变过程。结果表明,该模型有能力捕捉电化学腐蚀与机械变形之间复杂的相互作用,为各向异性材料从点蚀到开裂的转变提供了深入见解。所开发的相场数值模型在理解和模拟 SCC 现象方面取得了重大进展,有望应用于腐蚀问题严重的各个工程领域。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Computational Materials Science
工程技术-材料科学:综合
CiteScore
6.50
自引率
6.10%
发文量
665
审稿时长
26 days
期刊介绍:
The goal of Computational Materials Science is to report on results that provide new or unique insights into, or significantly expand our understanding of, the properties of materials or phenomena associated with their design, synthesis, processing, characterization, and utilization. To be relevant to the journal, the results should be applied or applicable to specific material systems that are discussed within the submission.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


