On the atomistic origin of internal length scale in strain-gradient plasticity models: The case of grain boundary structures and energies

Abstract

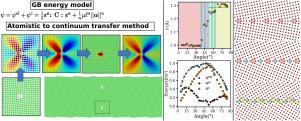
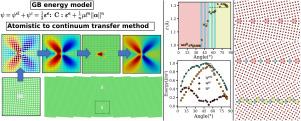
The mechanical behavior of polycrystalline materials is controlled by microstructural size effects such as grain size or precipitate size. Various models of strain gradient plasticity have been proposed to capture such size effects, many of which have incorporated geometrically-necessary dislocation (GND) densities to introduce characteristic internal lengths. Recent developments have focused on models that incorporate a GND density into the internal energy functional. In such models, one needs to physically justify the functional form chosen and quantify the inherent internal length parameter. Our present study aims at probing relevant forms and internal length values in the case of grain boundary (GB) atomistic structures and core energies. We use an atomistic-to-continuum crossover approach that predicts an atomistic structure dependent GB energy by molecular static simulations, which is then recovered at the continuum-level by using a strain gradient, atomistically informed, field dislocation mechanics fast Fourier transform model. This allows (i) delineating the atomistic structure of GBs using an equivalent Nye GND density, and (ii) capturing the associated continuous elastic fields in the GB core area. We probe (i) a generalized non-quadratic GND density dependent energy functional to account for the core energy of defects, and (ii) elucidate the contributions of core versus elastic energy to the overall GB excess energy. We investigate and discuss the possible relevant choices for the energy functional form, as well as the physical origin of the inherent internal length parameter and its dependence to the types of grain boundaries, atomistic structures, and spatial resolution.