Blending neural operators and relaxation methods in PDE numerical solvers
IF 18.8
1区 计算机科学
Q1 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE
引用次数: 0
Abstract
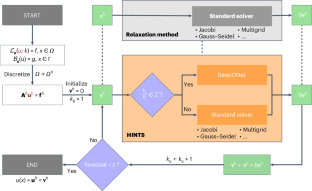
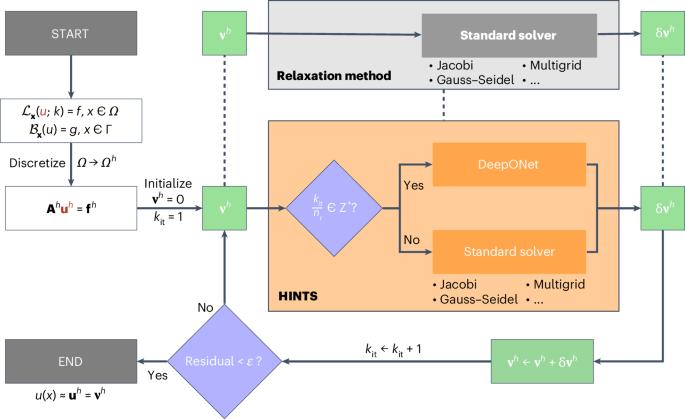
Neural networks suffer from spectral bias and have difficulty representing the high-frequency components of a function, whereas relaxation methods can resolve high frequencies efficiently but stall at moderate to low frequencies. We exploit the weaknesses of the two approaches by combining them synergistically to develop a fast numerical solver of partial differential equations (PDEs) at scale. Specifically, we propose HINTS, a hybrid, iterative, numerical and transferable solver by integrating a Deep Operator Network (DeepONet) with standard relaxation methods, leading to parallel efficiency and algorithmic scalability for a wide class of PDEs, not tractable with existing monolithic solvers. HINTS balances the convergence behaviour across the spectrum of eigenmodes by utilizing the spectral bias of DeepONet, resulting in a uniform convergence rate and hence exceptional performance of the hybrid solver overall. Moreover, HINTS applies to large-scale, multidimensional systems; it is flexible with regards to discretizations, computational domain and boundary conditions; and it can also be used to precondition Krylov methods. Neural-network-based solvers for partial differential equations (PDEs) suffer from difficulties tackling high-frequency modes when learning complex functions, whereas for classical solvers it is more difficult to handle low-frequency modes. Zhang and colleagues propose a hybrid numerical PDE solver by combining a Deep Operator Network with traditional relaxation methods, leading to balanced convergence across the eigenmode spectrum for a wide range of PDEs.
在 PDE 数值求解器中融合神经算子和松弛方法
神经网络存在频谱偏差,难以表现函数的高频分量,而松弛法可以高效地解决高频问题,但在中低频时会停滞不前。我们利用这两种方法的弱点,将它们协同结合起来,开发了一种大规模偏微分方程 (PDE) 的快速数值求解器。具体来说,我们提出的 HINTS 是一种混合、迭代、数值和可转移求解器,它将深度运算器网络(DeepONet)与标准松弛方法整合在一起,从而提高了并行效率和算法可扩展性,适用于多种现有单片求解器无法解决的偏微分方程。HINTS 利用 DeepONet 的频谱偏差,平衡了整个特征模式频谱的收敛行为,从而实现了统一的收敛速率,使混合求解器的整体性能出类拔萃。此外,HINTS 还适用于大规模、多维系统;在离散化、计算域和边界条件方面具有灵活性;还可用于对 Krylov 方法进行预处理。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Nature Machine Intelligence
Multiple-
CiteScore
36.90
自引率
2.10%
发文量
127
期刊介绍:
Nature Machine Intelligence is a distinguished publication that presents original research and reviews on various topics in machine learning, robotics, and AI. Our focus extends beyond these fields, exploring their profound impact on other scientific disciplines, as well as societal and industrial aspects. We recognize limitless possibilities wherein machine intelligence can augment human capabilities and knowledge in domains like scientific exploration, healthcare, medical diagnostics, and the creation of safe and sustainable cities, transportation, and agriculture. Simultaneously, we acknowledge the emergence of ethical, social, and legal concerns due to the rapid pace of advancements.
To foster interdisciplinary discussions on these far-reaching implications, Nature Machine Intelligence serves as a platform for dialogue facilitated through Comments, News Features, News & Views articles, and Correspondence. Our goal is to encourage a comprehensive examination of these subjects.
Similar to all Nature-branded journals, Nature Machine Intelligence operates under the guidance of a team of skilled editors. We adhere to a fair and rigorous peer-review process, ensuring high standards of copy-editing and production, swift publication, and editorial independence.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


