Solitary and traveling wave solutions to nematic liquid crystal equations using Jacobi elliptic functions
Q1 Mathematics
引用次数: 0
Abstract
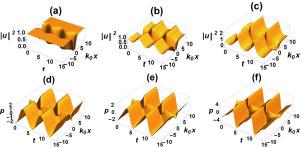
In our paper we apply the Jacobi elliptic function (JEF) expansion method to obtain exact solutions to the system of equations governing nematic liquid crystals, a system of high importance in nonlinear optics with numerous physical applications. We obtain solutions that are second-order polynomials in terms of JEFs for both the wave function and the tilt angle of molecular orientation. The solutions differ from previously obtained solutions in including both traveling and solitary wave solutions, with and without chirp. They also include the longitudinal dependence of coefficients in the equations, allowing for the management of both the dispersion and diffraction. Only two parameters of the differential equation need to be defined in terms of other coefficients, providing a wide range of flexibility when it comes to constructing solutions.
使用雅可比椭圆函数的向列液晶方程的孤波和行波解法
在我们的论文中,我们应用雅可比椭圆函数(JEF)展开法来获得向列液晶方程组的精确解,该方程组在非线性光学中具有重要意义,并有大量物理应用。我们得到的解是波函数和分子取向倾斜角的 JEF 二阶多项式。这些解与之前获得的解不同,既包括行波解,也包括孤波解,既有啁啾,也没有啁啾。它们还包括方程中系数的纵向依赖性,从而可以管理色散和衍射。微分方程中只有两个参数需要根据其他系数来定义,这为构建解法提供了广泛的灵活性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Chaos, Solitons and Fractals: X
Mathematics-Mathematics (all)
CiteScore
5.00
自引率
0.00%
发文量
15
审稿时长
20 weeks
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


