An explicit nonlinear model for large spatial deflections of symmetric slender beams

Abstract

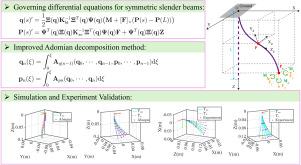
Flexible slender beams are commonly used in compliant mechanisms and continuum robots. However, the modeling of these beams can be complicated due to the geometric nonlinearity becoming significant at large elastic deflections. This paper presents an explicit nonlinear model for large spatial deflections of a slender beam with uniform, symmetrical sections subjected to general end-loading. The elongation, bending, torsion, and shear deformations of the beams are modeled based on Timoshenko’s assumptions and Cosserat rod theory. Subsequently, the nonlinear governing differential equations for the beam are derived from the quaternion representation of the rotation matrix. The explicit load–displacement relations of the beam are obtained using the improved Adomian decomposition method. This method is superior to the classical Adomian decomposition method in terms of convergence rate and domain. The convergence and superiority of the method are also rigorously demonstrated. Simulations are provided to verify the one-, two-, and three-dimensional deflections of beams. Real-world experiments have also been performed to validate our method’s effectiveness with two different beam configurations. The results indicate that the proposed method accurately estimates large spatial deflections of flexible beams.