Radial Positive Solutions for Semilinear Elliptic Problems with Linear Gradient Term in $$\mathbb {R}^N$$
引用次数: 0
Abstract
We are concerned with the linear problem
$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+\frac{\kappa }{|x|^2} x\cdot \nabla u =\lambda K(|x|) u, & x\in \mathbb {R}^N,\\ u(x)>0, & x\in \mathbb {R}^N,\\[2ex] u(x)\rightarrow 0, & |x|\rightarrow \infty , \end{array} \right. \end{aligned}$$where \(\lambda \) is a positive parameter, \(\kappa \in [0,N-2)\), \(N> 2\) and \(K:\mathbb {R}^N \rightarrow (0,\infty )\) is continuous and satisfies certain decay assumptions. We obtain the existence of the principal eigenvalue \(\lambda _1^{\text {rad}}\) and the corresponding positive eigenfunction \(\varphi _1\) satisfies \(\lim \nolimits _{|x|\rightarrow \infty }\varphi _1(|x|)=\frac{c}{|x|^{N-2-\kappa }}\) for some \(c>0\). As applications, we also study the existence of connected component of positive solutions for nonlinear infinite semipositone elliptic problems by bifurcation techniques.
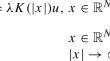
$$\mathbb{R}^N$$中带有线性梯度项的半线性椭圆问题的径向正解
我们关注的是线性问题 $$\begin{aligned}-\Delta u+frac{kappa }{|x|^2} x\cdot \nabla u =\lambda K(|x|) u, &;x\in \mathbb {R}^N,\ u(x)>0, & x\in \mathbb {R}^N,\[2ex] u(x)\rightarrow 0, & |x|rightarrow \infty , \end{array}.\right.\end{aligned}$$其中\(\lambda \)是一个正参数,\(\kappa \in [0,N-2)\), \(N> 2\) 和\(K:\mathbb {R}^N \rightarrow (0,\infty )\) 是连续的,并且满足某些衰变假设。我们得到了主特征值\(\lambda _1^{text {rad}}\)的存在性以及相应的正特征函数\(\varphi _1\)满足\(\lim \nolimits _{|x|\rightarrow \infty }\varphi _1(|x|)=\frac{c}{|x|^{N-2-\kappa }}\) for some \(c>0\).作为应用,我们还利用分岔技术研究了非线性无限半正交椭圆问题正解的连接部分的存在性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


