A Finite Difference informed Random Walk solver for simulating radiation defect evolution in polycrystalline structures with strongly inhomogeneous diffusivity

Abstract

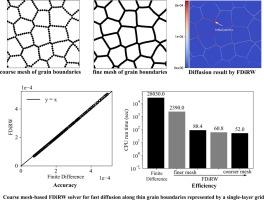
Diffusivity of species and defects on grain boundaries is usually several orders of magnitude larger than that inside grains. Such strongly inhomogeneous diffusivity requires prohibitively high computational demands for modeling microstructural evolution. This paper presents a highly efficient numerical solver, combining the Finite Difference method and Random Walk model, designed for accurately modeling strongly inhomogeneous diffusion within polycrystalline structures. The proposed solver, termed Finite Difference informed Random Walk (FDiRW), integrates a customized Finite Difference (cFD) scheme tailored for fast diffusion along thin grain boundaries represented by a single layer of nodes. Numerical experiments demonstrate that the FDiRW solver achieves an impressive efficiency gain of 1560x compared to traditional Finite Difference methods while maintaining accuracy, making it feasible for personal computer machines to handle diffusional systems with strongly inhomogeneous diffusivity across static polycrystalline microstructures. The model has been successfully applied to simulate radiation defect evolution, showcasing its scalability to engineering scales in both length and time dimensions.