Evidence of a finite-time pointlike singularity solution for the Euler equations for perfect fluids
IF 2.5
3区 物理与天体物理
Q2 PHYSICS, FLUIDS & PLASMAS
引用次数: 0
Abstract
This paper investigates the evolution of the Euler equations near a potential blow-up solution. We employ an approach where this solution exhibits second-type self-similarity, characterized by an undetermined exponent . This exponent can be seen as a nonlinear eigenvalue, determined by the solution of a self-similar partial differential equation with appropriate boundary conditions. Specifically, we demonstrate the existence of an axisymmetric solution of the Euler equations by expanding the axial vorticity using associated Legendre polynomials as a basis. This expansion results in an infinite hierarchy of ordinary differential equations, which, when truncated up to a certain order , allows for the numerical resolution of a finite set of ordinary differential equations. Through this numerical analysis, we obtain a solution that satisfies the appropriate boundary conditions for a specific value of the exponent . By exploring various truncations, we establish a sequence in for the parameter , providing evidence of the convergence of the exponent . Our findings suggest a self-similar exponent , presenting a promising path for a numerical or analytical approach indicating that may indeed be exactly 2.
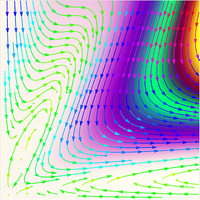
完美流体欧拉方程有限时间点状奇点解的证据
本文研究了欧拉方程在潜在爆炸解附近的演变。我们采用的方法是,该解表现出第二类自相似性,其特征是一个未确定的指数ν。该指数可视为一个非线性特征值,由具有适当边界条件的自相似偏微分方程的解决定。具体来说,我们以相关的 Legendre 多项式为基础,对轴向涡度进行扩展,从而证明欧拉方程轴对称解的存在。这种扩展导致了常微分方程的无限层次,当截断到一定阶次 N* 时,就可以对有限的常微分方程集进行数值解析。通过这种数值分析,我们得到了满足特定指数值 ν 的适当边界条件的解。通过探索各种截断,我们建立了参数 νN* 的 N* 序列,为指数 ν 的收敛提供了证据。我们的研究结果表明,ν≈2 是一个自相似的指数,这为数值或分析方法指明了一条大有可为的道路,表明 ν 确实可能正好是 2。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
Physical Review Fluids
Chemical Engineering-Fluid Flow and Transfer Processes
CiteScore
5.10
自引率
11.10%
发文量
488
期刊介绍:
Physical Review Fluids is APS’s newest online-only journal dedicated to publishing innovative research that will significantly advance the fundamental understanding of fluid dynamics. Physical Review Fluids expands the scope of the APS journals to include additional areas of fluid dynamics research, complements the existing Physical Review collection, and maintains the same quality and reputation that authors and subscribers expect from APS. The journal is published with the endorsement of the APS Division of Fluid Dynamics.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


