Evidence of a finite-time pointlike singularity solution for the Euler equations for perfect fluids

Abstract

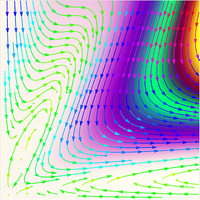
This paper investigates the evolution of the Euler equations near a potential blow-up solution. We employ an approach where this solution exhibits second-type self-similarity, characterized by an undetermined exponent $\nu$. This exponent can be seen as a nonlinear eigenvalue, determined by the solution of a self-similar partial differential equation with appropriate boundary conditions. Specifically, we demonstrate the existence of an axisymmetric solution of the Euler equations by expanding the axial vorticity using associated Legendre polynomials as a basis. This expansion results in an infinite hierarchy of ordinary differential equations, which, when truncated up to a certain order $N^{*}$, allows for the numerical resolution of a finite set of ordinary differential equations. Through this numerical analysis, we obtain a solution that satisfies the appropriate boundary conditions for a specific value of the exponent $\nu$. By exploring various truncations, we establish a sequence in $N^{*}$ for the parameter ${\nu }_{N^{*}}$, providing evidence of the convergence of the exponent $\nu$. Our findings suggest a self-similar exponent $\nu \approx 2$, presenting a promising path for a numerical or analytical approach indicating that $\nu$ may indeed be exactly 2.