Subcritical axisymmetric solutions in rotor-stator flow
IF 2.5
3区 物理与天体物理
Q2 PHYSICS, FLUIDS & PLASMAS
引用次数: 0
Abstract
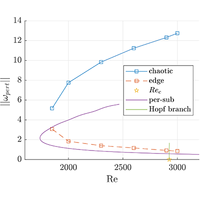
Rotor-stator cavity flows are known to exhibit unsteady flow structures in the form of circular and spiral rolls. While the origin of the spirals is well understood, that of the circular rolls is not. In the present study the axisymmetric flow in an aspect ratio cavity is revisited numerically using recent concepts and tools from bifurcation theory. It is confirmed that a linear instability takes place at a finite critical Reynolds number and that there exists a subcritical branch of large amplitude chaotic solutions. This motivates the search for subcritical finite-amplitude solutions. The branch of periodic states born in a Hopf bifurcation at , identified using a self-consistent method (SCM) and arclength continuation, is found to be supercritical. The associated solutions only exist, however, in a very narrow range of and do not explain the subcritical chaotic rolls. Another subcritical branch of periodic solutions is found using the harmonic balance method with an initial guess obtained by SCM. In addition, edge states separating the steady laminar and chaotic regimes are identified using a bisection algorithm. These edge states are biperiodic in time for most values of , where their dynamics is analyzed in detail. Both solution branches fold around at approximately the same value of , which is lower than yet still larger than the values reported in experiments. This suggests that, at least in the absence of external forcing, sustained chaotic rolls have their origin in the bifurcations from these unstable solutions.
转子-定子流动中的次临界轴对称解法
众所周知,转子-定子空腔流表现出圆形和螺旋形的不稳定流动结构。虽然螺旋的起源已为人熟知,但圆卷的起源尚不清楚。本研究利用分岔理论的最新概念和工具,对长径比 R/H=10 的空腔中的轴对称流动进行了数值研究。研究证实,在有限临界雷诺数 Re=Rec 时会出现线性不稳定性,并且存在大振幅混沌解的亚临界分支。这激发了对亚临界有限振幅解的探索。利用自洽方法(SCM)和 arclength continuation 确定了在 Re=Rec 处产生于霍普夫分岔的周期状态分支,发现它是超临界的。然而,相关解仅存在于 Re 非常窄的范围内,无法解释亚临界混沌辊。利用谐波平衡法和单片机获得的初始猜测,发现了周期解的另一个亚临界分支。此外,还利用分段算法确定了分隔稳定层流和混沌状态的边缘状态。在大多数 Re 值下,这些边缘状态在时间上是双周期的,对它们的动力学进行了详细分析。两个解分支在近似相同的 Re 值处折叠,该值低于 Rec 值,但仍大于实验报告的值。这表明,至少在没有外部强迫的情况下,持续的混沌滚动起源于这些不稳定解的分岔。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
Physical Review Fluids
Chemical Engineering-Fluid Flow and Transfer Processes
CiteScore
5.10
自引率
11.10%
发文量
488
期刊介绍:
Physical Review Fluids is APS’s newest online-only journal dedicated to publishing innovative research that will significantly advance the fundamental understanding of fluid dynamics. Physical Review Fluids expands the scope of the APS journals to include additional areas of fluid dynamics research, complements the existing Physical Review collection, and maintains the same quality and reputation that authors and subscribers expect from APS. The journal is published with the endorsement of the APS Division of Fluid Dynamics.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


