Translation of a sphere towards a rigid plane in an Oldroyd-B fluid
IF 2.5
3区 物理与天体物理
Q2 PHYSICS, FLUIDS & PLASMAS
引用次数: 0
Abstract
We analyze the low-Reynolds-number translation of a sphere towards or away from a rigid plane in an Oldroyd-B fluid under two scenarios: prescribing the sphere's translational velocity, and prescribing the force on the sphere. Leveraging the lubrication approximation and a perturbation expansion in powers of the Deborah number, we develop a comprehensive theoretical analysis that yields analytical approximations for velocity fields, pressures, and forces acting on the sphere. Our framework aids in understanding temporal microstructural changes as the particle-wall gap evolves over time. In particular, we show that alterations in the polymer conformation tensor in response to geometric changes induce additional forces on the sphere. For cases with prescribed velocity, we present a theoretical approach for calculating resistive forces at any order in the Deborah number and utilize a reciprocal theorem to obtain higher-order corrections based on velocity fields in the previous orders. When the sphere translates with a constant velocity, the fluid viscoelasticity decreases the resistive force at the first order. However, at the second-order correction, the direction of the sphere's movement determines whether viscoelasticity increases or decreases the resistive force. For cases with prescribed force, we show that understanding the influence of viscoelasticity on the sphere's translational velocity necessitates a more intricate analysis even at low Deborah numbers. Specifically, we introduce an ansatz for constant force scenarios, and we derive solution forms for general prescribed forces using the method of multiple scales. We find that when a sphere undergoes sedimentation due to its own weight, the fluid viscoelasticity results in a slower settling process, reducing the leading-order sedimentation rate.
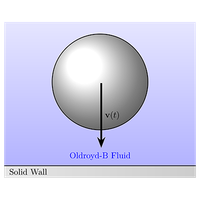
球体在奥尔德罗伊德-B 流体中向刚性平面的平移
我们分析了在奥尔德罗伊德-B 流体中球体朝向或远离刚性平面的低雷诺数平移的两种情况:规定球体的平移速度和规定球体上的力。利用润滑近似和德博拉数幂的扰动扩展,我们进行了全面的理论分析,得出了球体上的速度场、压力和作用力的分析近似值。我们的框架有助于理解颗粒-壁间隙随时间演变时的微观结构变化。我们特别指出,聚合物构象张量随几何变化而发生的改变会对球体产生额外的作用力。对于具有规定速度的情况,我们提出了一种理论方法,用于计算德博拉数任意阶的阻力,并利用倒易定理根据前阶速度场获得高阶修正。当球体以恒定速度平移时,流体粘弹性会降低一阶阻力。然而,在二阶修正时,球体的运动方向决定了粘弹性是增加还是减少阻力。对于有规定力的情况,我们表明,要理解粘弹性对球体平移速度的影响,就必须进行更复杂的分析,即使在低德博拉数的情况下也是如此。具体来说,我们引入了恒定力情况的解析,并利用多尺度方法推导出了一般规定力的求解形式。我们发现,当球体由于自身重量而发生沉降时,流体粘弹性会导致沉降过程变慢,从而降低前阶沉降速度。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
Physical Review Fluids
Chemical Engineering-Fluid Flow and Transfer Processes
CiteScore
5.10
自引率
11.10%
发文量
488
期刊介绍:
Physical Review Fluids is APS’s newest online-only journal dedicated to publishing innovative research that will significantly advance the fundamental understanding of fluid dynamics. Physical Review Fluids expands the scope of the APS journals to include additional areas of fluid dynamics research, complements the existing Physical Review collection, and maintains the same quality and reputation that authors and subscribers expect from APS. The journal is published with the endorsement of the APS Division of Fluid Dynamics.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


