Edge-wave phase shifts versus normal-mode phase tilts in an Eady problem with a sloping boundary
IF 2.5
3区 物理与天体物理
Q2 PHYSICS, FLUIDS & PLASMAS
引用次数: 0
Abstract
One mechanistic interpretation of baroclinic instability is that of mutual constructive interference of Rossby edge waves. The suppression of baroclinic instability over slopes has been widely established, where previous research argues that a sloping boundary modifies the properties of these Rossby edge waves, but does not provide a mechanistic explanation for the suppression that is valid over all parameter space. In the context of an Eady problem modified by the presence of a sloping boundary, we provide a mechanistic rationalization for baroclinic instability in the presence of slopes that is valid over all parameter space, via an equivalent formulation explicitly in terms of Rossby edge waves. We also highlight the differences between edge-wave phase shifts and normal-mode phase tilts, showing that the edge-wave phase shifts should be the ones that are mechanistically relevant, and normal-mode phase tilt is a potentially misleading quantity to use. Further, we present evidence that the edge-wave phase shifts but not normal-mode phase tilts are well correlated with geometric quantities diagnosed from an analysis framework based on eddy variance ellipses. The result is noteworthy in that the geometric framework makes no explicit reference to the edge-wave structures in its construction, and the correlation suggests the geometric framework can be used in problems where edge-wave structures are not so well defined or readily available. Some implications for parametrization of baroclinic instability and relevant eddy-mean feedbacks are discussed. For completeness, we also provide an explicit demonstration that the linear instability problem of the present modified Eady problem is parity-time symmetric, and speculate about some suggestive links between parity-time symmetry, shear instability, and the edge-wave interaction mechanism.
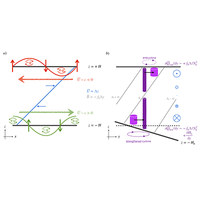
具有倾斜边界的埃迪问题中的边波相位偏移与正常模式相位倾斜的关系
对巴氏不稳定性的一种机理解释是罗斯比边缘波的相互建构干扰。斜坡上的巴氏不稳定性受到抑制的现象已被广泛证实,以往的研究认为斜坡边界改变了这些罗斯比边缘波的特性,但并没有提供在所有参数空间都有效的抑制机理解释。在因存在倾斜边界而有所改变的埃迪问题背景下,我们通过明确以罗斯比边缘波为基础的等效表述,为斜坡存在时的巴氏不稳定性提供了在所有参数空间内都有效的机理解释。我们还强调了边缘波相位移动和常模相位倾斜之间的差异,表明边缘波相位移动应该是与机理相关的相位移动,而常模相位倾斜则可能会误导我们使用。此外,我们还提出证据表明,边波相移而非正常模式相位倾斜与基于涡度方差椭圆的分析框架诊断出的几何量有很好的相关性。值得注意的是,几何框架在构建过程中没有明确提及边波结构,而这种相关性表明,几何框架可用于边波结构定义不明确或不容易获得的问题。我们讨论了气压不稳定性参数化和相关涡均反馈的一些影响。为完整起见,我们还明确证明了目前修正的埃迪问题的线性不稳定性问题是奇偶时对称的,并推测了奇偶时对称性、剪切不稳定性和边波相互作用机制之间的一些暗示性联系。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
Physical Review Fluids
Chemical Engineering-Fluid Flow and Transfer Processes
CiteScore
5.10
自引率
11.10%
发文量
488
期刊介绍:
Physical Review Fluids is APS’s newest online-only journal dedicated to publishing innovative research that will significantly advance the fundamental understanding of fluid dynamics. Physical Review Fluids expands the scope of the APS journals to include additional areas of fluid dynamics research, complements the existing Physical Review collection, and maintains the same quality and reputation that authors and subscribers expect from APS. The journal is published with the endorsement of the APS Division of Fluid Dynamics.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


