On the Gross–Prasad conjecture with its refinement for (SO(5), SO(2)) and the generalized Böcherer conjecture

IF 1.3 1区数学 Q1 MATHEMATICS

Compositio Mathematica Pub Date : 2024-09-13 DOI:10.1112/s0010437x24007267

Masaaki Furusawa, Kazuki Morimoto

{"title":"On the Gross–Prasad conjecture with its refinement for (SO(5), SO(2)) and the generalized Böcherer conjecture","authors":"Masaaki Furusawa, Kazuki Morimoto","doi":"10.1112/s0010437x24007267","DOIUrl":null,"url":null,"abstract":"We investigate the Gross–Prasad conjecture and its refinement for the Bessel periods in the case of <img data-mimesubtype=\"png\" data-type=\"\" src=\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20240912063150983-0859:S0010437X24007267:S0010437X24007267_inline2.png\">$(\\mathrm {SO}(5), \\mathrm {SO}(2))$</img>. In particular, by combining several theta correspondences, we prove the Ichino–Ikeda-type formula for any tempered irreducible cuspidal automorphic representation. As a corollary of our formula, we prove an explicit formula relating certain weighted averages of Fourier coefficients of holomorphic Siegel cusp forms of degree two, which are Hecke eigenforms, to central special values of <img data-mimesubtype=\"png\" data-type=\"\" src=\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20240912063150983-0859:S0010437X24007267:S0010437X24007267_inline3.png\">$L$</img>-functions. The formula is regarded as a natural generalization of the Böcherer conjecture to the non-trivial toroidal character case.","PeriodicalId":55232,"journal":{"name":"Compositio Mathematica","volume":null,"pages":null},"PeriodicalIF":1.3000,"publicationDate":"2024-09-13","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Compositio Mathematica","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1112/s0010437x24007267","RegionNum":1,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

Abstract

We investigate the Gross–Prasad conjecture and its refinement for the Bessel periods in the case of 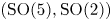Abstract Image $(\mathrm {SO}(5), \mathrm {SO}(2))$. In particular, by combining several theta correspondences, we prove the Ichino–Ikeda-type formula for any tempered irreducible cuspidal automorphic representation. As a corollary of our formula, we prove an explicit formula relating certain weighted averages of Fourier coefficients of holomorphic Siegel cusp forms of degree two, which are Hecke eigenforms, to central special values of 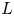Abstract Image $L$-functions. The formula is regarded as a natural generalization of the Böcherer conjecture to the non-trivial toroidal character case.

查看原文本刊更多论文

关于格罗斯-普拉萨德猜想及其对（SO(5), SO(2)）的完善和广义伯切尔猜想

我们研究了在 $(\mathrm {SO}(5), \mathrm {SO}(2))$ 的情况下贝塞尔周期的格罗斯-普拉萨德猜想及其细化。特别是，通过结合几种θ对应关系，我们证明了任何回火不可还原尖顶自形表示的伊奇诺-池田式公式。作为我们公式的一个推论，我们证明了一个明确的公式，它将二度全形西格尔凹凸形式（即赫克特征形式）的某些加权平均傅里叶系数与 $L$ 函数的中心特异值联系起来。该公式被视为伯切尔猜想在非三重环状特征情况下的自然推广。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Compositio Mathematica 数学-数学

CiteScore

2.10

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： Compositio Mathematica is a prestigious, well-established journal publishing first-class research papers that traditionally focus on the mainstream of pure mathematics. Compositio Mathematica has a broad scope which includes the fields of algebra, number theory, topology, algebraic and differential geometry and global analysis. Papers on other topics are welcome if they are of broad interest. All contributions are required to meet high standards of quality and originality. The Journal has an international editorial board reflected in the journal content.