ON A PROBLEM OF PONGSRIIAM ON THE SUM OF DIVISORS

Abstract

For any positive integer n, let 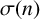$\sigma (n)$ be the sum of all positive divisors of n. We prove that for every integer k with 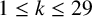$1\leq k\leq 29$ and 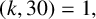$(k,30)=1,$ 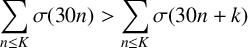$$ \begin{align*} \sum_{n\leq K}\sigma(30n)>\sum_{n\leq K}\sigma(30n+k) \end{align*} $$

for all 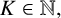$K\in \mathbb {N},$ which gives a positive answer to a problem posed by Pongsriiam [‘Sums of divisors on arithmetic progressions’, Period. Math. Hungar. 88 (2024), 443–460].