Optimal $$L^{2}$$ -growth of the generalized Rosenau equation
IF 1.3
3区 数学
Q2 MATHEMATICS
Journal of Pseudo-Differential Operators and Applications
Pub Date : 2024-08-26
DOI:10.1007/s11868-024-00635-w
引用次数: 0
Abstract
We report that the quantity measured in the \(L^2\) norm of the solution itself of the generalized Rosenau equation, which was completely unknown in this equation, grows in the proper order at time infinity. It is also immediately apparent that this growth aspect does not occur in three or more spatial dimensions, so we will apply the results obtained in this study to provide another proof that Hardy-type inequalities do not hold in the case of one or two spatial dimensions.
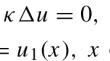
广义罗森奥方程的最优 $$L^{2}$$ - 增长
我们报告说,广义罗森奥方程的解本身的 \(L^2\) norm 所测量的量在这个方程中是完全未知的,它在时间无穷大时以适当的阶次增长。同样显而易见的是,这种增长不会发生在三维或更多维的空间中,因此我们将应用本研究中获得的结果再次证明哈代型不等式在一维或两维的空间中不成立。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Pseudo-Differential Operators and Applications
MATHEMATICS, APPLIED-MATHEMATICS
CiteScore
2.20
自引率
9.10%
发文量
59
期刊介绍:
The Journal of Pseudo-Differential Operators and Applications is a forum for high quality papers in the mathematics, applications and numerical analysis of pseudo-differential operators. Pseudo-differential operators are understood in a very broad sense embracing but not limited to harmonic analysis, functional analysis, operator theory and algebras, partial differential equations, geometry, mathematical physics and novel applications in engineering, geophysics and medical sciences.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


