Vanishing theorem for Hodge ideals on smooth hypersurfaces
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
We use a Koszul-type resolution to prove a weak version of Bott’s vanishing theorem for smooth hypersurfaces in \(\mathbb {P}^n\) and use this result to prove a vanishing theorem for Hodge ideals associated to an effective Cartier divisor on a hypersurface. This extends an earlier result of Mustaţă and Popa.
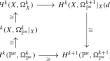
光滑超曲面上霍奇理想的消失定理
我们利用科斯祖尔型解析证明了 Bott's vanishing theorem 的弱版本,即在\(\mathbb {P}^n\) 中的光滑超曲面的消失定理,并利用这一结果证明了与超曲面上有效卡蒂埃除数相关的霍奇理想的消失定理。这扩展了穆斯塔法和波帕的一个早期结果。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.60
自引率
0.00%
发文量
236
审稿时长
3-6 weeks
期刊介绍:
"Mathematische Zeitschrift" is devoted to pure and applied mathematics. Reviews, problems etc. will not be published.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


