Dirichlet problems with fractional competing operators and fractional convection

IF 2.5 2区数学 Q1 MATHEMATICS

Fractional Calculus and Applied Analysis Pub Date : 2024-09-04 DOI:10.1007/s13540-024-00331-y

Laura Gambera, Salvatore Angelo Marano, Dumitru Motreanu

引用次数: 0

Abstract

In this paper, the existence of weak solutions to some Dirichlet problems with fractional competing operators and distributional Riesz fractional gradient is investigated. Due to the nature of driving operators, the most known techniques, basically based on ellipticity and monotonicity, are no longer applicable. Generalized solutions (in a suitable sense) are obtained via an approximation procedure and a corollary of the Brouwer fixed point theorem.

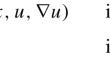
Abstract Image

查看原文本刊更多论文

带分数竞争算子和分数对流的 Dirichlet 问题

本文研究了一些具有分数竞争算子和分布式 Riesz 分数梯度的 Dirichlet 问题的弱解存在性。由于驱动算子的性质，基本基于椭圆性和单调性的已知技术不再适用。通过近似程序和布劳威尔定点定理的推论，可以获得广义解（在适当的意义上）。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Fractional Calculus and Applied Analysis MATHEMATICS, APPLIED-MATHEMATICS, INTERDISCIPLINARY APPLICATIONS

CiteScore

4.70

自引率

16.70%

发文量

101

期刊介绍： Fractional Calculus and Applied Analysis (FCAA, abbreviated in the World databases as Fract. Calc. Appl. Anal. or FRACT CALC APPL ANAL) is a specialized international journal for theory and applications of an important branch of Mathematical Analysis (Calculus) where differentiations and integrations can be of arbitrary non-integer order. The high standards of its contents are guaranteed by the prominent members of Editorial Board and the expertise of invited external reviewers, and proven by the recently achieved high values of impact factor (JIF) and impact rang (SJR), launching the journal to top places of the ranking lists of Thomson Reuters and Scopus.