Spin Space Groups: Full Classification and Applications

Abstract

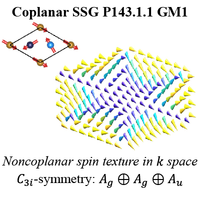
In this work, we exhaust all the spin space symmetries, which fully characterize collinear, noncollinear, and commensurate spiral as well as incommensurate spiral magnetism, etc., and investigate enriched features of electronic bands that respect these symmetries. We achieve this by systematically classifying the so-called spin space groups (SSGs)—joint symmetry groups of spatial and spin operations that leave the magnetic structure unchanged. Generally speaking, they are accurate (approximate) symmetries in systems where spin-orbit coupling (SOC) is negligible (finite but weaker than the energy scale of interest), but we also show that specific SSGs could remain valid even in the presence of strong SOC. In recent years, SSGs have played increasingly pivotal roles in various fields such as altermagnetism, topological electronic states, and topological magnon, etc. However, due to its complexity, a complete SSG classification has not been completed up to now. By representing the SSGs as $\mathrm{O}(N)$ representations, we—for the first time—obtain the complete classifications of 1421, 9542, and 56 512 distinct SSGs for collinear ($N=1$), coplanar ($N=2$), and noncoplanar ($N=3$) magnetism, respectively. SSG not only fully characterizes the symmetry of spin degrees of freedom, but also gives rise to exotic electronic states, which, in general, form projective representations of magnetic space groups (MSGs). Surprisingly, electronic bands in SSGs exhibit features never seen in MSGs, such as (i) nonsymmorphic SSG Brillouin zone, where SSG operations behave as a glide or screw when acting on momentum, (ii) effective $\pi$ flux, where translation operators anticommute with each other and yield duplicate bands, (iii) higher-dimensional representations unexplained by MSGs, and (iv) unconventional spin texture on a Fermi surface, which is completely determined by SSGs, independent of Hamiltonian details. To apply our theory, we identify the SSG for each of the 1595 published magnetic structures in the MAGNDATA database on the Bilbao Crystallographic Server. Material examples exhibiting the novel features (i)–(iv) are discussed with emphasis. We also investigate new types of SSG-protected topological electronic states that are unprecedented in MSGs. In particular, we propose a 3D ${\mathbb{Z}}_2$ topological insulator state with a fourfold degenerate Dirac point on the surface and a new scenario of anomalous ${\mathbb{Z}}_2$ helical states that appear on magnetic domain walls.