Learning integral operators via neural integral equations

Abstract

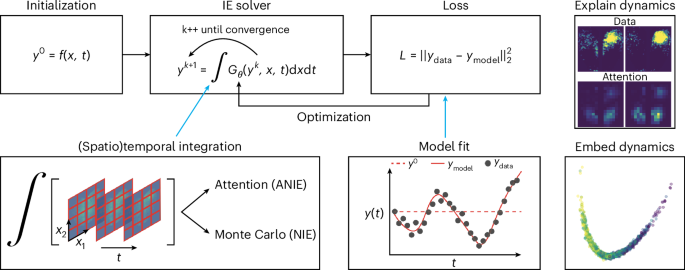
Nonlinear operators with long-distance spatiotemporal dependencies are fundamental in modelling complex systems across sciences; yet, learning these non-local operators remains challenging in machine learning. Integral equations, which model such non-local systems, have wide-ranging applications in physics, chemistry, biology and engineering. We introduce the neural integral equation, a method for learning unknown integral operators from data using an integral equation solver. To improve scalability and model capacity, we also present the attentional neural integral equation, which replaces the integral with self-attention. Both models are grounded in the theory of second-kind integral equations, where the indeterminate appears both inside and outside the integral operator. We provide a theoretical analysis showing how self-attention can approximate integral operators under mild regularity assumptions, further deepening previously reported connections between transformers and integration, as well as deriving corresponding approximation results for integral operators. Through numerical benchmarks on synthetic and real-world data, including Lotka–Volterra, Navier–Stokes and Burgers’ equations, as well as brain dynamics and integral equations, we showcase the models’ capabilities and their ability to derive interpretable dynamics embeddings. Our experiments demonstrate that attentional neural integral equations outperform existing methods, especially for longer time intervals and higher-dimensional problems. Our work addresses a critical gap in machine learning for non-local operators and offers a powerful tool for studying unknown complex systems with long-range dependencies. Integral equations are used in science and engineering to model complex systems with non-local dependencies; however, existing traditional and machine-learning-based methods cannot yield accurate or efficient solutions in several complex cases. Zappala and colleagues introduce a neural-network-based method that can learn an integral operator and its dynamics from data, demonstrating higher accuracy or scalability compared with several state-of-the-art methods.