On some fractional parabolic reaction-diffusion systems with gradient source terms
IF 2.9
2区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
The present paper is concerned with a fractional parabolic reaction-diffusion system posed in a regular bounded open subset of \({\mathbb {R}}^N\), where the gradients of the unknowns act as source terms (see (S) below). First, we establish some nonexistence and blow-up in finite time results. Second, we prove some new weighted regularity results. Such results are interesting in themselves and play a crucial role to study local existence of nonnegative solutions to our system under suitable assumptions on the data. This work also highlights a substantial difference between the nonlocal case and the local case already studied by the fourth author and his coworkers.
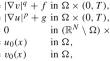
关于一些带有梯度源项的分数抛物线反应扩散系统
本文关注的是在\({\mathbb {R}}^N\) 的规则有界开放子集中提出的分数抛物面反应扩散系统,其中未知数的梯度作为源项(见下文 (S))。首先,我们建立了一些不存在和在有限时间内炸毁的结果。其次,我们证明了一些新的加权正则性结果。这些结果本身就很有趣,而且对研究我们系统在适当数据假设下非负解的局部存在性起着至关重要的作用。这项工作还凸显了非局部情况与第四作者及其同事已经研究过的局部情况之间的本质区别。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Fractional Calculus and Applied Analysis
MATHEMATICS, APPLIED-MATHEMATICS, INTERDISCIPLINARY APPLICATIONS
CiteScore
4.70
自引率
16.70%
发文量
101
期刊介绍:
Fractional Calculus and Applied Analysis (FCAA, abbreviated in the World databases as Fract. Calc. Appl. Anal. or FRACT CALC APPL ANAL) is a specialized international journal for theory and applications of an important branch of Mathematical Analysis (Calculus) where differentiations and integrations can be of arbitrary non-integer order. The high standards of its contents are guaranteed by the prominent members of Editorial Board and the expertise of invited external reviewers, and proven by the recently achieved high values of impact factor (JIF) and impact rang (SJR), launching the journal to top places of the ranking lists of Thomson Reuters and Scopus.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


