Generalized double affine Hecke algebra for double torus

IF 1.3 3区物理与天体物理 Q3 PHYSICS, MATHEMATICAL

Letters in Mathematical Physics Pub Date : 2024-08-07 DOI:10.1007/s11005-024-01848-2

Kazuhiro Hikami

引用次数: 0

Abstract

We propose a generalization of the double affine Hecke algebra of type-\(C^\vee C_1\) at specific parameters by introducing a “Heegaard dual” of the Hecke operators. Shown is a relationship with the skein algebra on double torus. We give automorphisms of the algebra associated with the Dehn twists on the double torus.

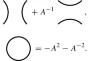
Abstract Image

查看原文本刊更多论文

双环的广义双仿射赫克代数

我们通过引入赫克算子的 "希加德对偶"，提出了在特定参数下类型为-(C^\vee C_1\)的双仿射赫克代数的一般化。这说明了它与双环上的斯金代数的关系。我们给出了与双环上的德恩捻相关的代数的自动形态。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Letters in Mathematical Physics 物理-物理：数学物理

CiteScore

2.40

自引率

8.30%

发文量

111

审稿时长

3 months

期刊介绍： The aim of Letters in Mathematical Physics is to attract the community''s attention on important and original developments in the area of mathematical physics and contemporary theoretical physics. The journal publishes letters and longer research articles, occasionally also articles containing topical reviews. We are committed to both fast publication and careful refereeing. In addition, the journal offers important contributions to modern mathematics in fields which have a potential physical application, and important developments in theoretical physics which have potential mathematical impact.