Approximate derivation of the power law for the mean streamwise velocity in a turbulent boundary layer under zero-pressure gradient

Abstract

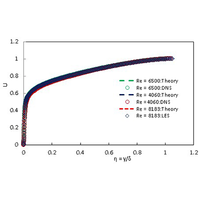
Distribution of the mean streamwise velocity in a turbulent boundary layer over a flat plate can be represented by the equation $U\sim {\eta }^{1/n}$, as was widely used in the past; $U$ and $\eta$ are the normalized velocity and the wall-normal distance, respectively. However, this $1/n\mathrm{th}$-power law is an empirical one. By incorporating either the Reynolds shear stress model of Wei et al. [J. Fluid Mech. 969, A3 (2023)], which is in terms of $U$ and the (normalized) wall-normal velocity ($V$), or a similar one in the boundary layer equations, it is found that $U$ and $V$ are related as $U^{(H+1)}\sim V^{(H-1)}$ in the outer region of a flat plate boundary layer; $H$ is the flow shape parameter. Along with the distribution of the wall-normal velocity ($V_w$) of Wei et al., the $1/n\mathrm{th}$-power law for $U$ is obtained by equating the derivative (with respect to $\eta$) of $V$ with that of $V_w$. Thus, this empirical power law seems to have a reasonable theoretical basis embedded in it.