Estimates of discrete time derivatives for the parabolic-parabolic Robin-Robin coupling method

IF 1.7 3区数学 Q2 MATHEMATICS, APPLIED

Numerical Algorithms Pub Date : 2024-08-09 DOI:10.1007/s11075-024-01902-z

Erik Burman, Rebecca Durst, Miguel A. Fernández, Johnny Guzmán, Sijing Liu

引用次数: 0

Abstract

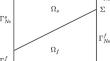
We consider a loosely coupled, non-iterative Robin-Robin coupling method proposed and analyzed in Burman et al. (J. Numer. Math. 31(1):59–77, 2023) for a parabolic-parabolic interface problem and prove estimates for the discrete time derivatives of the scalar field in different norms. When the interface is flat and perpendicular to two of the edges of the domain we prove error estimates in the \(H^2\)-norm. Such estimates are key ingredients to analyze a defect correction method for the parabolic-parabolic interface problem. Numerical results are shown to support our findings.

Abstract Image

查看原文本刊更多论文

抛物线-抛物线罗宾-罗宾耦合法的离散时间导数估算

我们考虑 Burman 等人（J. Numer. Math.Math.31(1):59-77, 2023）中提出并分析的抛物线-抛物线界面问题，并证明了不同规范下标量场离散时间导数的估计值。当界面平坦且垂直于域的两条边时，我们证明了在\(H^2\)规范下的误差估计。这些估计值是分析抛物线-抛物线界面问题缺陷修正方法的关键要素。数值结果表明支持我们的发现。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Numerical Algorithms 数学-应用数学

CiteScore

4.00

自引率

9.50%

发文量

201

审稿时长

9 months

期刊介绍： The journal Numerical Algorithms is devoted to numerical algorithms. It publishes original and review papers on all the aspects of numerical algorithms: new algorithms, theoretical results, implementation, numerical stability, complexity, parallel computing, subroutines, and applications. Papers on computer algebra related to obtaining numerical results will also be considered. It is intended to publish only high quality papers containing material not published elsewhere.