Continuous Equality Knapsack with Probit-Style Objectives

IF 16.4 1区化学 Q1 CHEMISTRY, MULTIDISCIPLINARY

Accounts of Chemical Research Pub Date : 2024-08-12 DOI:10.1007/s10957-024-02503-5

Jamie Fravel, Robert Hildebrand, Laurel Travis

引用次数: 0

Abstract

We study continuous, equality knapsack problems with uniform separable, non-convex objective functions that are continuous, antisymmetric about a point, and have concave and convex regions. For example, this model captures a simple allocation problem with the goal of optimizing an expected value where the objective is a sum of cumulative distribution functions of identically distributed normal distributions (i.e., a sum of inverse probit functions). We prove structural results of this model under general assumptions and provide two algorithms for efficient optimization: (1) running in linear time and (2) running in a constant number of operations given preprocessing of the objective function.

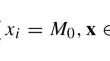
Abstract Image

查看原文本刊更多论文

带有 Probit 类型目标的连续等价包

我们研究的是连续、相等、具有均匀可分、非凸目标函数的knapsack问题，这些目标函数是连续的、关于一点的非对称的，并且有凹和凸区域。例如，该模型捕捉了一个简单的分配问题，其目标是优化预期值，目标函数是同分布正态分布的累积分布函数之和（即逆概率函数之和）。我们证明了该模型在一般假设下的结构性结果，并提供了两种高效优化算法：(1) 在线性时间内运行；(2) 在对目标函数进行预处理的情况下，以恒定的运算次数运行。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Accounts of Chemical Research 化学-化学综合

CiteScore

31.40

自引率

1.10%

发文量

312

审稿时长

2 months

期刊介绍： Accounts of Chemical Research presents short, concise and critical articles offering easy-to-read overviews of basic research and applications in all areas of chemistry and biochemistry. These short reviews focus on research from the author’s own laboratory and are designed to teach the reader about a research project. In addition, Accounts of Chemical Research publishes commentaries that give an informed opinion on a current research problem. Special Issues online are devoted to a single topic of unusual activity and significance. Accounts of Chemical Research replaces the traditional article abstract with an article "Conspectus." These entries synopsize the research affording the reader a closer look at the content and significance of an article. Through this provision of a more detailed description of the article contents, the Conspectus enhances the article's discoverability by search engines and the exposure for the research.