The $$P=W$$ identity for isolated cluster varieties: full rank case
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
We initiate a systematic construction of real analytic Lagrangian fibrations from integer matrices. We prove that when the matrix is of full column rank, the perverse filtration associated with the Lagrangian fibration matches the mixed Hodge-theoretic weight filtration of the isolated cluster variety associated with the matrix.
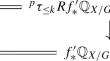
孤立群集品种的 $$P=W$$ 特性:全秩情况
我们从整数矩阵出发,系统地构建了实解析拉格朗日纤维。我们证明,当矩阵为全列秩时,与拉格朗日纤维相关的反滤波与与矩阵相关的孤立簇品种的混合霍奇理论权滤波相匹配。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.60
自引率
0.00%
发文量
236
审稿时长
3-6 weeks
期刊介绍:
"Mathematische Zeitschrift" is devoted to pure and applied mathematics. Reviews, problems etc. will not be published.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


