Many Equiprojective Polytopes
IF 0.6
3区 数学
Q4 COMPUTER SCIENCE, THEORY & METHODS
引用次数: 0
Abstract
A 3-dimensional polytope P is k-equiprojective when the projection of P along any line that is not parallel to a facet of P is a polygon with k vertices. In 1968, Geoffrey Shephard asked for a description of all equiprojective polytopes. It has been shown recently that the number of combinatorial types of k-equiprojective polytopes is at least linear as a function of k. Here, it is shown that there are at least \(k^{3k/2+o(k)}\) such combinatorial types as k goes to infinity. This relies on the Goodman–Pollack lower bound on the number of order types of point configurations and on new constructions of equiprojective polytopes via Minkowski sums.
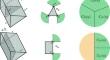
许多等射多边形
当一个三维多边形 P 沿着与 P 的一个面不平行的任何线的投影是一个有 k 个顶点的多边形时,这个多边形 P 是 k 等投影的。1968 年,杰弗里-谢泼德(Geoffrey Shephard)要求描述所有等投影多面体。最近的研究表明,k 等投影多边形的组合类型数量至少是 k 的线性函数。这里的研究表明,当 k 变为无穷大时,至少有 \(k^{3k/2+o(k)}\) 个这样的组合类型。这依赖于古德曼-波拉克(Goodman-Pollack)关于点配置阶类型数量的下限,以及通过闵科夫斯基和对等投影多面体的新构造。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Discrete & Computational Geometry
数学-计算机:理论方法
CiteScore
1.80
自引率
12.50%
发文量
99
审稿时长
6-12 weeks
期刊介绍:
Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


