Nonlocal to Local Convergence of Phase Field Systems with Inertial Term
IF 1.6
2区 数学
Q2 MATHEMATICS, APPLIED
引用次数: 0
Abstract
This paper deals with a nonlocal model for a hyperbolic phase field system coupling the standard energy balance equation for temperature with a dynamic for the phase variable: the latter includes an inertial term and a nonlocal convolution-type operator where the family of kernels depends on a small parameter. We rigorously study the asymptotic convergence of the system as the approximating parameter tends to zero and we obtain at the limit the local system with the elliptic laplacian operator acting on the phase variable. Our analysis is based on some asymptotic properties on nonlocal-to-local convergence that have been recently and successfully applied to families of Cahn–Hilliard models.
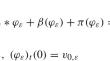
带惯性项的相场系统从非局部到局部的收敛性
本文论述了双曲相场系统的非局部模型,该模型将温度的标准能量平衡方程与相变的动态方程耦合在一起:后者包括惯性项和非局部卷积型算子,其中的核族取决于一个小参数。我们严格研究了当近似参数趋近于零时系统的渐近收敛性,并在极限处得到了带有作用于相变的椭圆拉普拉斯算子的局部系统。我们的分析基于最近成功应用于 Cahn-Hilliard 模型族的一些非局部到局部收敛的渐近特性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.30
自引率
5.60%
发文量
103
审稿时长
>12 weeks
期刊介绍:
The Applied Mathematics and Optimization Journal covers a broad range of mathematical methods in particular those that bridge with optimization and have some connection with applications. Core topics include calculus of variations, partial differential equations, stochastic control, optimization of deterministic or stochastic systems in discrete or continuous time, homogenization, control theory, mean field games, dynamic games and optimal transport. Algorithmic, data analytic, machine learning and numerical methods which support the modeling and analysis of optimization problems are encouraged. Of great interest are papers which show some novel idea in either the theory or model which include some connection with potential applications in science and engineering.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


